
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 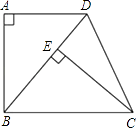
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
【答案】
(1)证明:∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,
∵∠A=∠CEB,AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠BCE,
又∵BC=BD
∴△ABD≌△ECB
(2)解:∵∠DBC=50°,BC=BD,
∴∠EDC= ![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCE=90°﹣∠EDC=90°﹣65°=25°.

【解析】(1)因为这两个三角形是直角三角形,BC=BD,因为AD∥BC,还能推出∠ADB=∠EBC,从而能证明:△ABD≌△ECB.(2)因为∠DBC=50°,BC=BD,可求出∠BDC的度数,进而求出∠DCE的度数.
【考点精析】关于本题考查的直角梯形,需要了解一腰垂直于底的梯形是直角梯形才能得出正确答案.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图. 
(1)本次抽测的男生有人,抽测成绩的众数是;
(2)请你将图2的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°. 
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m). (参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个结论中,正确的是( )
A.方程x+ ![]() =﹣2有两个不相等的实数根
=﹣2有两个不相等的实数根
B.方程x+ ![]() =1有两个不相等的实数根
=1有两个不相等的实数根
C.方程x+ ![]() =2有两个不相等的实数根
=2有两个不相等的实数根
D.方程x+ ![]() =a(其中a为常数,且|a|>2)有两个不相等的实数根
=a(其中a为常数,且|a|>2)有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是边长为4的正方形,以AB为直径在正方形内作半圆,P是半圆上的动点(不与点A、B重合),连接PA、PB、PC、PD. 
(1)如图①,当PA的长度等于时,∠PAD=60°;当PA的长度等于时,△PAD是等腰三角形;
(2)如图②,以AB边所在直线为x轴、AD边所在直线为y轴,建立如图所示的直角坐标系(点A即为原点O),把△PAD、△PAB、△PBC的面积分别记为S1、S2、S3 . 设P点坐标为(a,b),试求2S1S3﹣S22的最大值,并求出此时a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(1,0)、B(0,﹣1)、C(﹣1,2)、D(2,﹣1)、E(4,2)五个点,抛物线y=a(x﹣1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x﹣1)2+k(a>0)上;
(2)点A在抛物线y=a(x﹣1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下. 
(1)求训练后第一组平均成绩比训练前增长的百分数;
(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;
(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com