
【题目】
(1)解不等式:2x﹣3≤ ![]() (x+2)
(x+2)
(2)解方程组: ![]() .
.
【答案】
(1)解:2x﹣3≤ ![]() (x+2)
(x+2)
去分母得:4x﹣6≤x+2,
移项,合并同类项得:3x≤8,
系数化为1得:x≤ ![]()
(2)解: ![]() .
.
由①得:2x+y=3③,
③×2﹣②得:x=4,
把x=4代入③得:y=﹣5,
故原方程组的解为 ![]()
【解析】(1)根据解一元一次不等式的步骤,去分母、移项、合并同类项、系数化为1,即可得出结果;(2)用加减法消去未知数y求出x的值,再代入求出y的值即可.
【考点精析】本题主要考查了解二元一次方程组和一元一次不等式的解法的相关知识点,需要掌握二元一次方程组:①代入消元法;②加减消元法;步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题)才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 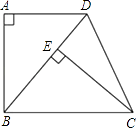
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,坐标原点O是正方形OABC的一个顶点,已知点B坐标为(1,7),过点P(a,0)(a>0)作PE⊥x轴,与边OA交于点E(异于点O、A),将四边形ABCE沿CE翻折,点A′、B′分别是点A、B的对应点,若点A′恰好落在直线PE上,则a的值等于( ) 
A.![]()
B.![]()
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90° 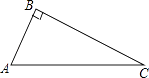
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母) ①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC
(2)判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3 
(1)求A、B两点的坐标;
(2)若tan∠PDB= ![]() ,求这个二次函数的关系式.
,求这个二次函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图. 最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点C(3,0),函数y= ![]() (k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(1)求m的值;
(2)若△OAD的面积等于6,求k的值;
(3)若P为函数y═ ![]() (k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当
(k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当 ![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则Sn的值为 . (用含n的代数式表示,n为正整数) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com