
【题目】如图,平面直角坐标系xOy中,点C(3,0),函数y= ![]() (k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(1)求m的值;
(2)若△OAD的面积等于6,求k的值;
(3)若P为函数y═ ![]() (k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当
(k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当 ![]() 时,求t的值.
时,求t的值.
【答案】
(1)
解:∵点C(3,0),OABC的顶点A(m,n),
∴B(m+3,n),
∴D( ![]() +3,
+3, ![]() ),
),
∵函数y= ![]() (k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D,
(k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D,
∴mn=k, ![]() ,
,
∴m=2
(2)
解:∵点D是平行四边形BC中点,
∴S平行四边形OABC=2S△OAD=12,
∵S平行四边形OABC=3×n=12,
∴n=4,
由(1)知,m=2,
∴k=mn=8
(3)
解:①如图1,点N在OA上,
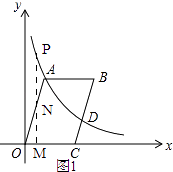
由(1)知,m=2,
∴A(2,n).
即0<t<2
直线OA的解析式为y= ![]() x,
x,
设点P的横坐标为t,
∴P(t, ![]() ),
),
∵过点P作直线l⊥x轴于点M.
∴N(t, ![]() t),M(t,0),
t),M(t,0),
∴PN= ![]() ﹣
﹣ ![]() t,PM=
t,PM= ![]() ,
,
∵ ![]() ,
,
∴ ![]() =4(
=4( ![]() ﹣
﹣ ![]() t),
t),
∴t= ![]() 或t=﹣
或t=﹣ ![]() (舍),
(舍),
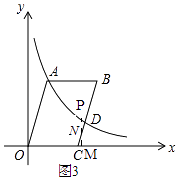
②如图2,

当点N在AB上时,
由(1)知,B(5,n),
∴2≤t≤3
由题意知,P(t, ![]() ).N(t,n),M(t,0),
).N(t,n),M(t,0),
∵ ![]() ,
,
∴4(n﹣ ![]() )=
)= ![]() ,
,
∴t= ![]() ,
,
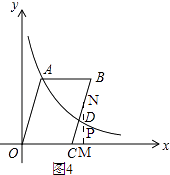
当点N在BC上时,(3<t≤5)
∵B(5,n),C(3,0),
∴直线BC解析式为y= ![]() x﹣
x﹣ ![]() ,
,
∴P(t, ![]() ),N(t,
),N(t, ![]() t﹣
t﹣ ![]() ),M(t,0),
),M(t,0),
∵ ![]() ,
,
∴4| ![]() t﹣
t﹣ ![]() ﹣
﹣ ![]() |=
|= ![]() ,
,
∴t= ![]() 或t=
或t= ![]() (舍)或t=
(舍)或t= ![]() 或t=
或t= ![]() (舍)
(舍)
∴t的值为 ![]() ,
, ![]() ,
, ![]() 或
或 ![]()
【解析】(1)根据平行四边形的性质确定出B的坐标从而确定出D的坐标,而点A,D在反比例函数图象上,建立方程求出m,(2)根据三角形OAD的面积是平行四边形OABC面积的一半,确定出n即可;(3)根据平行四边形的性质和双曲线的性质,确定出PM,ON即可.
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


科目:初中数学 来源: 题型:
【题目】某校部分男生分3组进行引体向上训练.对训练前后的成绩进行统计分析,相应数据的统计图如下. 
(1)求训练后第一组平均成绩比训练前增长的百分数;
(2)小明在分析了图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多.”你同意小明的观点吗?请说明理由;
(3)你认为哪一组的训练效果最好?请提供一个解释来支持你的观点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场新进一批水果,有苹果、西瓜、桃子和香蕉四个品种,统计后将结果绘制成条形图(如图),已知西瓜的重量占这批水果总重量的40%. 回答下列问题:
(1)这批水果总重量为kg;
(2)请将条形图补充完整;
(3)若用扇形图表示统计结果,则桃子所对应扇形的圆心角为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数y=x2+bx的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为2 ![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1 , 求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1 , 求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a﹣2b+c的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高. 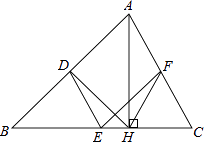
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com