
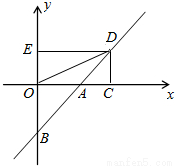
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证:AD•BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.
(1)证明见解析;(2)证明见解析;(3)存在,y=x-1.
【解析】
试题分析:(1)由于DE⊥y轴,DC⊥x轴,不难得出∠EDC=90°,因此要证AD平分∠CDE,需证得∠ADC或∠ADE为45°,根据直线AB的解析式可得出A(-b,0),B(0,b),因此OA=OB,即三角形OAB是等腰直角三角形,即可证得∠ADC=∠ABO=45°,由此可得证;
(2)在(1)中已经证得三角形ADC是等腰三角形,同理可得出三角形BDE也是等腰三角形,因此AD=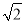 CD,BD=
CD,BD=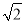 DE,那么AD•BD=2CD•DE,而CD和DE的长,正好是反比例函数图象上D点的横坐标与纵坐标,由此可得出AD•BD是个定值;
DE,那么AD•BD=2CD•DE,而CD和DE的长,正好是反比例函数图象上D点的横坐标与纵坐标,由此可得出AD•BD是个定值;
(3)如果四边形OBCD是平行四边形,需要满足的条件是OB=CD,OA=AC,可根据这个条件设B、D的坐标,然后将D点坐标代入反比例函数的解析式中,即可求出D点坐标,也就得出了B点的坐标,然后用待定系数法即可求得直线的解析式.
试题解析:(1)证明:由y=x+b得A(-b,0),B(0,b).
∴∠DAC=∠OAB=45°
又∵DC⊥x轴,DE⊥y轴
∴∠ACD=∠CDE=90°
∴∠ADC=45°
即AD平分∠CDE.
(2)证明:∵∠ACD=90°,∠ADC=45°,
∴△ACD是等腰直角三角形,
同理可得,△BDE是等腰直角三角形,
∴AD=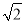 CD,BD=
CD,BD=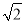 DE.
DE.
∴AD•BD=2CD•DE=2×2=4为定值.
(3)【解析】
存在直线AB,使得OBCD为平行四边形.
若OBCD为平行四边形,则AO=AC,OB=CD.
由(1)知AO=BO,AC=CD,
设OB=a(a>0),
∴B(0,-a),D(2a,a),
∵D的横纵坐标之积为2,
∴点D在双曲线y=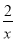 上,
上,
∴2a•a=2,
∴a1=-1(舍去),a2=1,
∴B(0,-1).
又∵B在y=x+b上,
∴b=-1.
即存在直线:y=x-1,使得四边形OBCD为平行四边形.
考点:1.一次函数综合题;2.等腰直角三角形;3.平行四边形的判定与性质.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源:2015届河南省平顶山市八年级下学期期中考试数学试卷(解析版) 题型:选择题
已知不等式ax+b<0的解集是x< - 2,下列有可能是直线y =ax+b的图象是( )
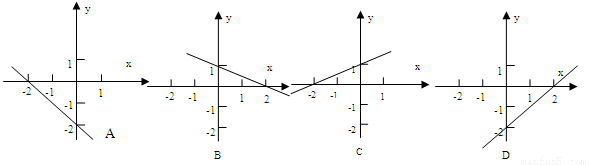
查看答案和解析>>
科目:初中数学 来源:2015届河南平顶山华英学校八年级下学级第一次月考数学试卷(解析版) 题型:选择题
某数的2倍加上5不大于这个数的3倍减去4,那么该数的范围是[ ].
A.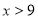 B.
B.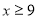 C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市赵县八年级下学期期末考试数学试卷(解析版) 题型:解答题
我国是一个严重缺水的国家,为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费,该市某户居民5月份用水x吨,应交水费y元.
(1)请写出y与x的函数关系式.
(2)如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市八年级下学期期末考试数学试卷(解析版) 题型:解答题
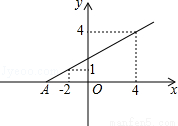
已知一次函数图象如图:
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一点,且点A为该函数图象与x轴的交点,若S△PAO=6,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com