
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=-![]() x2+3x+1的一部分,如图.
x2+3x+1的一部分,如图.
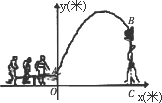
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
|
思路点拨:(1)抓住关键词“最大高度”,我们会想到将二次函数化成顶点式,演员弹跳离地面的最大高度也就是图象的最大值;(2)正确理解“表演成功与否”的含义,从数学角度看,实质上是看人梯的最高点的坐标是否是(4,3.4).如果是,则成功,不是,则不成功.通过代入数值可以进行判断. 解:(1)y=- 因为- 答:演员弹跳的最大高度是 (2)当x=4时,y=- 所以这次表演成功. 点评:本题主要考查二次函数的性质和图象.解本题的关键是正确理解题意,灵活运用二次函数的有关知识求解. |


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
 看成一点)的路线是抛物线y=-
看成一点)的路线是抛物线y=-| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 看成一点)的路线是抛物线y=-
看成一点)的路线是抛物线y=-| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
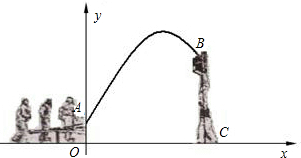
 如图,杂技团进行杂技表演,演员从跷跷板右端A处跳到人梯顶端椅子B处,其身体的路线是抛物线y=-
如图,杂技团进行杂技表演,演员从跷跷板右端A处跳到人梯顶端椅子B处,其身体的路线是抛物线y=-| 3 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 杂技团进行杂技表演,演员从跷跷板右端的A处弹跳到人梯顶端椅子B处,其身体(看成一点)运动的路线是抛物线y=-
杂技团进行杂技表演,演员从跷跷板右端的A处弹跳到人梯顶端椅子B处,其身体(看成一点)运动的路线是抛物线y=-| 3 |
| 5 |
| 17 |
| 5 |
| 17 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:2012届浙江省杭州市九年级上期第一次月考数学试卷(解析版) 题型:解答题
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线 的一部分,如图.
的一部分,如图.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com