
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
【答案】(1)y=![]() x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
x+1. (2)点C为线段AP的中点. (3)存在点D,使四边形BCPD为菱形,点D(8,1)即为所求.
【解析】试题分析:(1)由点A与点B关于y轴对称,可得AO=BO,再由A的坐标求得B点的坐标,从而求得点P的坐标,将P坐标代入反比例解析式求出m的值,即可确定出反比例解析式,将A与P坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式;(2)由AO=BO,PB∥CO,即可证得结论 ;(3)假设存在这样的D点,使四边形BCPD为菱形,过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
的图象于点D,分别连结PD、BD,如图所示,即可得点D(8,1), BP⊥CD,易证PB与CD互相垂直平分,即可得四边形BCPD为菱形,从而得点D的坐标.
试题解析:
(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(-4,0),
∴B(4,0),
∴P(4,2),
把P(4,2)代入y=![]() 得m=8,
得m=8,
∴反比例函数的解析式:y=![]()
把A(-4,0),P(4,2)代入y=kx+b
得: ![]() ,解得:
,解得: ![]() ,
,
所以一次函数的解析式:y=![]() x+1.
x+1.
(2)∵点A与点B关于y轴对称,
∴OA=OB
∵PB丄x轴于点B,
∴∠PBA=90°,
∵∠COA=90°,
∴PB∥CO,
∴点C为线段AP的中点.
(3)存在点D,使四边形BCPD为菱形
∵点C为线段AP的中点,
∴BC= ![]() ,
,
∴BC和PC是菱形的两条边
由y=![]() x+1,可得点C(0,1),
x+1,可得点C(0,1),
过点C作CD平行于x轴,交PB于点E,交反比例函数y=![]() 的图象于点D,
的图象于点D,
分别连结PD、BD,
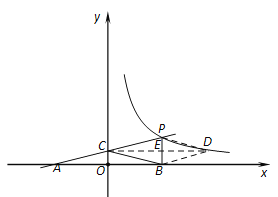
∴点D(8,1), BP⊥CD
∴PE=BE=1,
∴CE=DE=4,
∴PB与CD互相垂直平分,
∴四边形BCPD为菱形.
∴点D(8,1)即为所求.


科目:初中数学 来源: 题型:
【题目】某校决定在4月7日开展“世界无烟日”宣传活动,活动有A.社区板报、B.集会演讲、C.喇叭广播、D.发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:


请结合统计图表,回答下列问题:
(1)本次抽查的学生共______人,m=____________,并将条形统计图补充完整;
(2)若该校学生有1500人,请你估计该校喜欢“集会演讲”这项宣传方式的学生约有多少人?
(3)学校采用抽签方式让每班在A、B、C、D四种宣传方式中随机抽取两种进行展示,请用树状图或列表法求某班所抽到的两种方式恰好是“集会演讲”和“喇叭广播”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的一半(木条宽度忽略不计),则这个平行四边形的最小内角为度.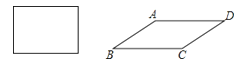
查看答案和解析>>
科目:初中数学 来源: 题型:
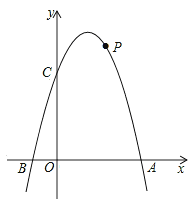
【题目】如图,已知二次函数y=﹣x2+bx+c的图象交x轴于点A(4,0)和点B,交y轴于点C(0,4).
(1)求这个二次函数的表达式;
(2)若点P在第一象限内的抛物线上,求四边形AOCP面积的最大值和此时点P的坐标;
(3)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+px+q=0的两个根为x1=3,x2=﹣4,则二次三项式x2﹣px+q可分解为( )
A. (x+3)(x﹣4)B. (x﹣3)(x+4)C. (x+3)(x+4)D. (x﹣3)(x﹣4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com