
已知:如图①,在矩形ABCD中,AB=5,AD= ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB、AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角 (0°<
(0°< <180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P.与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.

(1)4,3;(2)当点F在线段AB上时,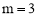 ;当点F在线段AD上时,
;当点F在线段AD上时,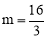 ;
;
(3)存在,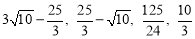 .
.
【解析】
试题分析:(1)由勾股定理求得BD的长,根据三角形面积公式求出AE的长,再应用勾股定理即可求得BE的长.
(2)根据平移的性质求解即可.
(3)分DP=DQ(考虑点Q在线段BD的延长线和点Q在线段BD上两种情况),QP=QD,PD=PQ三种情况求解即可.
试题解析:(1)∵AB=5,AD= ,∴由勾股定理得
,∴由勾股定理得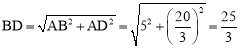 .
.
∵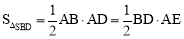 ,∴
,∴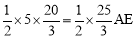 ,解得AE=4.
,解得AE=4.
∴ .
.
(2)当点F在线段AB上时,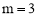 ;当点F在线段AD上时,
;当点F在线段AD上时,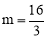 .
.
(3)存在,理由如下:
①当DP=DQ时,若点Q在线段BD的延长线上时,如答图1,有∠Q=∠1,则∠2=∠1+∠Q=2∠Q.
∵∠3=∠4+∠Q,∠3=∠2,∴∠4+∠Q=2∠Q.∴∠4=∠Q.
∴A′Q=A′B=5.∴F′Q=4+5=9.
在Rt△BF′Q中,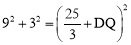 ,解得
,解得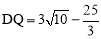 或
或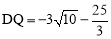 (舍去).
(舍去).
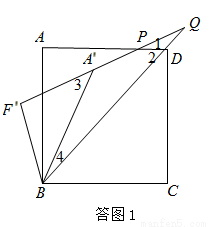
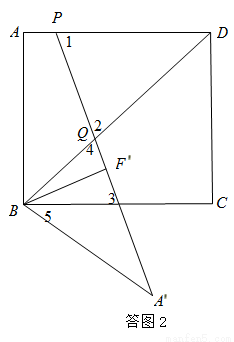
若点Q在线段BD上时,如答图2,有∠1=∠2=∠4,
∵∠1=∠3,∴∠3=∠4.
∵∠3=∠5+∠A′,∠A′=∠CBD,∴∠3=∠5+∠CBD=∠A′BQ.∴∠4=∠∠A′BQ.∴A′Q= A′B=5.
∴F′Q=5-4=1.∴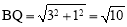 .∴
.∴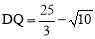 .
.
②当QP=QD时,如答图3,有∠P=∠1,
∵∠A′=∠1,∠2=∠3,∴∠4=∠P.∴∠4=∠A′.∴QB=Q A′.
设QB=Q A′=x,
在Rt△BF′Q中,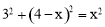 设备,解得
设备,解得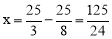 .
.
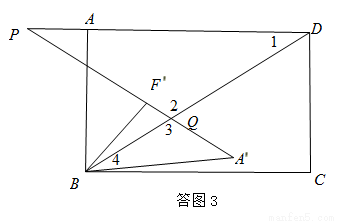
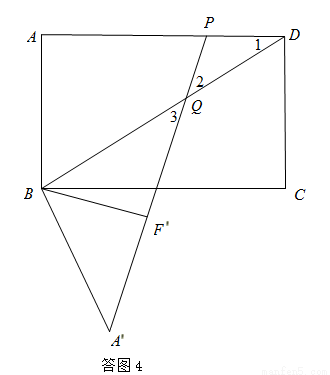
③当PD=PQ时,如答图4,有∠1=∠2=∠3,
∵∠1=∠A′,∴∠3=∠A′.∴BQ=A′B=5.
∴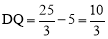 .
.
综上所述,当△DPQ为等腰三角形时,DQ的长为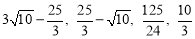 .
.
考点:1.轴对称、平移和旋转问题;2.矩形的性质;3.勾股定理;4.等腰三角形存在性问题;5.勾股定理;6.分类思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:选择题
哈市某天的最高气温为28℃,最低气温为21℃,则这一天的最高气温与最低气温的差为( )
A.5℃ B.6℃ C.7℃ D.8℃
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:填空题
2014年6月4日据经济日报报道:青海格尔木枸杞已进入国际市场,远销美国、欧盟、东南亚等国家和地区,出口创汇达4000000美元,将4000000美元用科学记数法表示为 美元.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:选择题
如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )

A.中 B.钓 C.鱼 D.岛
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:填空题
据有关部门统计,截止到2014年5月1日,重庆市私家小轿车已达到563 000辆,将563 000这个数用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:解答题
“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣

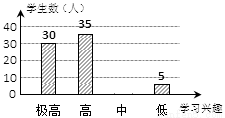
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:选择题
若一粒米的质量约是0.000012kg,将数据0.000012用科学记数法表示为( )
A.12×10-4 B.1.2×10-6 C.1.2×10-5 D.1.2×10-4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com