
分析 利用点D在OB上,得到BD=1,然后分类讨论:当点在⊙O外,OD=OB+BD=3,在Rt△COD中,利用勾股定理可计算出CD=$\sqrt{13}$;当点在⊙O内,OD′=OB-BD′=1,利用勾股定理可计算出CD′=$\sqrt{5}$,于是得到CD的长为$\sqrt{5}$或$\sqrt{13}$.
解答 解:如图,∵直径AB=4,
∴OB=2,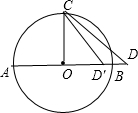 ∵OC⊥AB,
∵OC⊥AB,
∴∠COB=90°,
∵点D与圆O上各点所连接线段最短为1,
∴BD=1,
当点在⊙O外,OD=OB+BD=2+1=3,
在Rt△COD中,CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\sqrt{13}$;
当点在⊙O内,OD′=OB-BD′=2-1=1,
在Rt△COD中,CD′=$\sqrt{O{C}^{2}+OD{′}^{2}}$=$\sqrt{5}$,
∴CD的长为$\sqrt{5}$或$\sqrt{13}$.
故答案为$\sqrt{5}$或$\sqrt{13}$.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了勾股定理.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
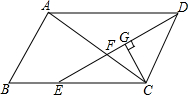 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com