
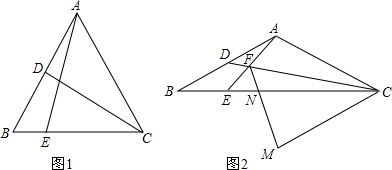
分析 (1)由于要证的结论是一个线段比例关系,因此可以过A点作平行线,根据平行线成比例或相似得出相关比例等式,再适当运算即可得证.
(2)由于告诉了特殊角120度,各线段位置固定,只要设定一条线段,其也所有线段可解,因此可考虑用代数法计算出或表示出EN和MF,那么它们的数量关系自然明了.
解答 解:(1)过点A作AG∥BC,交CD的延长线于点G,如图1: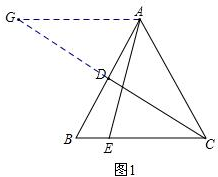
∵AG∥BC,
∴∠DGA=∠DCB,∠DAG=∠DBC,
在△DAG与△DBC中,
$\left\{\begin{array}{l}{∠DGA=∠DCB}\\{∠DAG=∠DBC}\\{AD=BD}\end{array}\right.$,
∴△DAG≌△DBC(AAS),
∴AG=BC,
又∵AG∥BC,
∴$\frac{AF}{EF}=\frac{AG}{EC}$,
∵BE=$\frac{1}{4}$BC,
∴$\frac{BC}{EC}=\frac{4}{3}$,
∴$\frac{AG}{EC}=\frac{4}{3}$,
∴$\frac{AF}{EF}=\frac{4}{3}$,
即EF=$\frac{3}{4}$AF.
(2)如图2,过点A作AP⊥BC于P,过点C作CH⊥BA于H,延长MF交AB于K,过点D作DR∥BC交AE于R,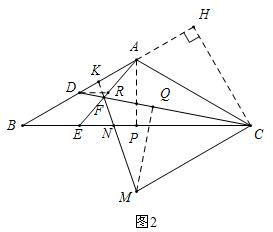
∵AB=AC,∠BAC=120,
∴CP=BP,∠ABC=∠ACB=30°,
设AP=2,则AB=AC=4,BP=CP=2$\sqrt{3}$,
∵∠BAC=120°,
∴∠HAC=60°,
∴AH=2,CH=2$\sqrt{3}$,
∵D为AB中点,
∴AD=BD=2,
∵BE=$\frac{1}{4}$BC,BP=$\frac{1}{2}$BC,
∴EP=BE=$\sqrt{3}$,
∴DE=$\frac{1}{2}$AP=1,CE=3$\sqrt{3}$,
∴CD=2$\sqrt{7}$,
∴$\frac{EP}{AP}=\frac{\sqrt{3}}{2}$,$\frac{CH}{DH}=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}$,
∴∠CDH=∠EAP,
∴∠AFC=∠CDH+∠BAE=∠EAP+∠BAE=60°,
根据翻折性质可知∠MFC=∠AFC=60°,∠MCB=∠ACB=30°,
∴∠ACM=60°,
∴A、F、M、C四点共圆,(如果不用四点共圆,只需截取FL=FA,证△CLF与△CAF全等即可同样得出CM=CA)
∵∠MFC=∠AFC,
∴CM=AC=4,
∵DR∥BC,D为AB中点,
∴DR=$\frac{1}{2}$BE=$\frac{1}{6}$CE,
∴$\frac{DF}{CF}=\frac{DR}{CE}=\frac{1}{6}$,
∵∠ABC=∠MCB=30°,
∴AB∥CM,
∴$\frac{DK}{CM}=\frac{DF}{CF}=\frac{1}{6}$,
∴DK=$\frac{1}{6}$CM=$\frac{2}{3}$,DF=$\frac{2}{7}$$\sqrt{7}$,CF=$\frac{12}{7}$$\sqrt{7}$,
∴BK=BD+DK=$\frac{8}{3}$,
∴$\frac{BN}{CN}=\frac{BK}{CM}=\frac{2}{3}$,
∴BN=$\frac{2}{5}$BC=$\frac{8\sqrt{3}}{5}$,
∴EN=BN-BE=$\frac{3\sqrt{3}}{5}$,
过点M作MQ⊥CF于点Q,
设FQ=x,则FM=2x,MQ=$\sqrt{3}$x,CQ=$\frac{12}{7}$$\sqrt{7}$-x,
∴($\sqrt{3}$x)2+($\frac{12}{7}$$\sqrt{7}$-x)2=16,
即:7x2-6$\sqrt{7}$x+8=0,解得:x=$\frac{2\sqrt{7}}{7}$(舍)或x=$\frac{4\sqrt{7}}{7}$
∴MF=2x=$\frac{8\sqrt{7}}{7}$
∴$\frac{MF}{EN}=\frac{40\sqrt{21}}{63}$.
点评 本题考查了平行线分线段成比例、相似三角形的判定及性质、翻折的性质、全等三角形的判定与性质、等腰三角形的性质、解三角形、勾股定理等众多知识点,综合性很强.巧妙作出辅助线、确定∠AFC=60°、正确计算出各线段长度是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
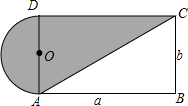 设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,
设计一个商标图案(如图阴影部分),其中O为半圆的圆心,AB=a,BC=b,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com