练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系xOy中，过坐标原点O的直线l与双曲线y= 相交于点A（m，3）．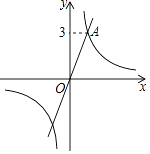
    （1）求直线l的表达式；
    （2）过动点P（n，0）且垂于x轴的直线与l及双曲线的交点分别为B，C，当点B位于点C上方时，写出n的取值范围 ．

    【答案】
    （1）解：∵双曲线y= 过点A（m，3），

    ∴3=3m，解得：m=1，

    ∴点A的坐标为（1，3）．

    设直线l的表达式为y=kx，

    将（1，3）代入y=kx中，3=k，

    ∴直线l的表达式为y=3x


    （2）解：﹣1＜n＜0或n＞1
    【解析】解： （2）由正、反比例函数的对称性可知：直线l与双曲线y= 的两交点坐标为（﹣1，﹣3）和（1，3）． 观察函数图象可知：当﹣1＜x＜0或x＞1时，一次函数图象在双曲线的上方，
    ∴n的取值范围为﹣1＜n＜0或n＞1．
    所以答案是：﹣1＜n＜0或n＞1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某厂工人小王某月工作的部分信息如下：

    信息一：工作时间：每天上午8：00～12：00，下午14：00～18：00，每月25天；

    信息二：生产甲、乙两种产品，并且按规定每月生产甲产品的件数不少于45件.

    生产产品件数与所用时间之间的关系见下表：

    生产甲产品件数（件）

    生产乙产品件数（件）

    所用总时间（分）

    10

    10

    500

    15

    20

    900

    信息三：按件计酬，每生产一件甲产品可得6元，每生产一件乙产品可得10元.

    根据以上信息，回答下列问题：

    (1)小王每生产一件甲种产品，每生产一件乙种产品分别需要多少分？

    (2)小王该月最多能得多少元？此时生产甲、乙两种产品分别多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AB=AC，∠A=30°，以B为圆心，BC长为半径画弧，分别交AC，AB于D，E两点，并连结BD，DE． 则∠BDE的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，一次函数 与反比例函数 的图象在第一象限的交点为A（1，n）．

    （1）求m与n的值；
    （2）设一次函数的图象与x轴交于点B，连结OA，求∠BAO的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AC和直线l分别垂直线段AB于点A，B．点P是线段AB上的一个动点，由A移动到B，连接CP，过点P作PD⊥CP交l于点D，设线段AP的长为x，BD的长为y，在下列图象中，能大致表示y与x之间函数关系的是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】太阳影子定位技术是通过分析视频中物体的太阳影子变化，确定视频拍摄地点的一种方法．为了确定视频拍摄地的经度，我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻．在一定条件下，直杆的太阳影子长度l（单位：米）与时刻t（单位：时）的关系满足函数关系l=at2+bt+c（a，b，c是常数），如图记录了三个时刻的数据，根据上述函数模型和记录的数据，则该地影子最短时，最接近的时刻t是（ ）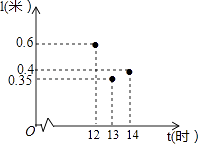
    A.12.75
    B.13
    C.13.33
    D.13.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC，以AB为直径的⊙O分别交AC，BC于点D，E，过点A作⊙O的切线交BC的延长线于点F，连接AE．
    （1）求证：∠ABC=2∠CAF；
    （2）过点C作CM⊥AF于M点，若CM=4，BE=6，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论： ①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1 ，
    其中正确的是 ．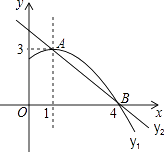

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点B、E、C、F在一条直线上，AB=DF，AC=DF，BE=FC．
    （1）求证：△ABC≌△DFE；
    （2）连接AF、BD，求证：四边形ABDF是平行四边形．

    查看答案和解析>>

    同步练习册答案