
【题目】太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法.为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻.在一定条件下,直杆的太阳影子长度l(单位:米)与时刻t(单位:时)的关系满足函数关系l=at2+bt+c(a,b,c是常数),如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是( ) 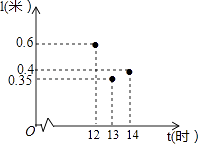
A.12.75
B.13
C.13.33
D.13.5
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作对DE⊥AB于点E,点F在边CD上,CF=AE,连结AF,BF. 
(1)求证:四边形BFDE是矩形.
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.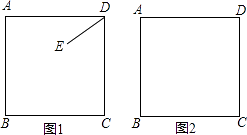
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过坐标原点O的直线l与双曲线y= ![]() 相交于点A(m,3).
相交于点A(m,3). 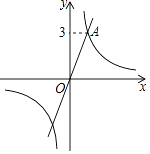
(1)求直线l的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l及双曲线的交点分别为B,C,当点B位于点C上方时,写出n的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y= ![]() x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 . 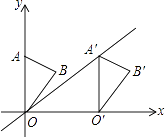
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2). 
(1)求这两个函数的表达式;
(2)观察图象,直接写出y1>y2时自变量x的取值范围.
(3)连接OA、OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义: 数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹); 
(2)如图2,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= ![]() CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用:
CD,试判断△AEF是否为“智慧三角形”,并说明理由; 运用: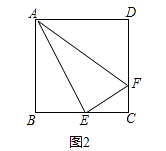
(3)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时点P的坐标. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com