
 用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少?
用一段长24m的篱笆围成一个一边靠墙的矩形菜园,墙长为15m,这个矩形长、宽各为多少时,菜园面积最大,最大面积是多少? 科目:初中数学 来源: 题型:选择题
| A. | a2 | B. | $\frac{1}{2}$a2 | C. | $\frac{1}{4}$a2 | D. | 以上答案都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
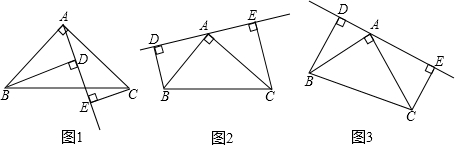
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
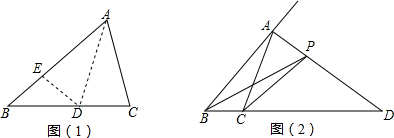
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
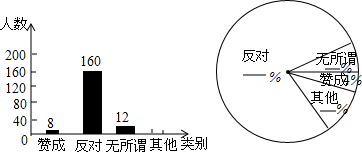
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程:
,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com