
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,
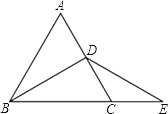
(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
【答案】(1)证明见解析;(2)48.
【解析】
(1)根据△ABC是等边三角形,BD是中线,可知∠DBC=30°,由CE=CD,∠ACD=60°可求得∠DCE=30°,即∠DBC=∠DCE,则DB=DE;
(2)根据Rt△DCF中∠FCD=30°知CD=2CF=4,即可知AC=8,则可求出△ABC的周长.
(1)解:证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED= ![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
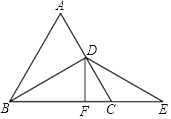
(2)解: ∵∠CDE=∠CED= ![]() ∠BCD=30°,DF⊥BE.
∠BCD=30°,DF⊥BE.
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.


科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:如何计算平面直角坐标系中任意两点之间的距离?
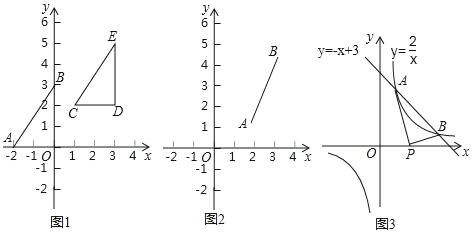
探究问题:
为解决上面的问题,我们从最简单的问题进行研究.
探究一:在图1中,已知线段AB,A(﹣2,0),B(0,3),写出线段AO的长,BO的长,所以线段AB的长为多少;把Rt△AOB向右平移3个单位,再向上平移2个单位,得到Rt△CDE,写出Rt△CDE的顶点坐标C,D,E,此时线段CD的长为多少,DE的长为多少,所以线段CE的长为多少.
探究二:在图2中,已知线段AB的端点坐标为A(a,b),B(c,d),求出图中AB的长(用含a,b,c,d的代数式表示,不必证明).
归纳总结:无论线段AB处于直角坐标系中的哪个位置,当其端点坐标为A(x1,y1),B(x2,y2)时线段AB的长为多少(用含x1,y1,x2,y2的代数式表示,不必证明).
拓展与应用:
运用在图3中,一次函数y=﹣x+3与反比例函数y=![]() 的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
的图象交点为A、B,交点的坐标分别是A(1,2),B(2,1).
①求线段AB的长;
②若点P是x轴上动点,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个各位数字都不为0的三位正整数N,现从它的百位、十位、个位上的数字中任意选择两个数字组成两位数若所有这些两位数的和等于这个三位数本身,则称这个三位数为本原数”例如:132,选择百位数字1和十位数字3所组成的两位数为:13和31;选择百位数字1和个位数字2所组成的两位数为:12和21;选择十位数字3和个位数字2所组成的两位数为:32和23,因为13+31+12+21+32+23=132,所以132是“本原数”
(1)判断123是不是“本原数”?请说明理由;
(2)一个三位正整数,若它的十位数字等于百位数字与个位数学的和,则称这样的三位数为“和中数”.若一个各位数字都不为0的“和中数”![]() 是“本原数”,求z与x的函数关系.
是“本原数”,求z与x的函数关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线y= ![]() 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且![]() .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
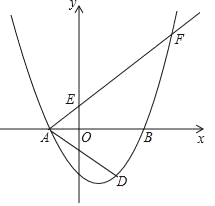
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小华和小夏玩掷骰子游戏,他们约定:他们用同一枚质地均匀的骰子各掷一次, 如果两次掷的骰子的点数相同则小华获胜:如果两次掷的骰子的点数的和是6则小夏获胜.
(1)请您列表或画树状图列举出所有可能出现的结果;
(2)请你判断这个游戏对他们是否公平并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
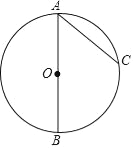
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF满足下列条件,其中能使△ABC与△DEF相似的是( )
A. AB=c,AC=b,BC=a,DE=![]() ,EF=
,EF=![]() ,DF=
,DF=![]()
B. AB=1,AC=1.5,BC=2,DE=12,EF=8,DF=1
C. AB=3,AC=4,BC=6,DE=12,EF=8,DF=6
D. AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,DE=
,DE=![]() ,EF=3,DF=3
,EF=3,DF=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com