
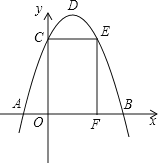
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,则△ABD的面积为_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
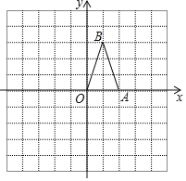
【题目】如图,在平面直角坐标系中,已知点A(2,0),点B(1,3).
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1,B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2mx +m-4 (m≠0)的顶点为A,与x轴交于B,C两点(B在点C左侧),与y轴交于点D.
(1)求点A的坐标;
(2)若BC=4,
①求抛物线的解析式;
②将抛物线在C,D之间的部分记为图象G (包含C,D两点) . 若过点A的直线y= kx+ b(k≠0)与图象G有两个交点,结合函数的图象,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=![]()
的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
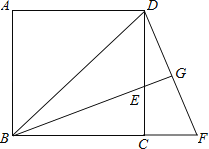
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
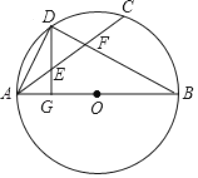
【题目】如图,AB为⊙O直径,D为弧AC的中点,DG⊥AB于G,交AC于E,AC、BD相交于F.
(1)求证:AE=DE;
(2)若AG=2,DG=4,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com