
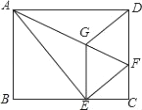
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论: ①DG=DF; ②四边形EFDG是菱形; ③![]() ;
;
④当![]() 时,BE的长为
时,BE的长为![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】试题解析:∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.故①正确;
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.故②正确;
如图1所示:连接DE,交AF于点O.
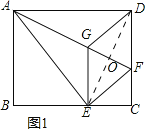
∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.故③正确;
GFAF.故③正确;
如图2所示:过点G作GH⊥DC,垂足为H.
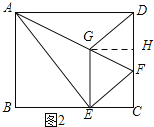
∵EG2=![]() GFAF,AG=6,EG=2
GFAF,AG=6,EG=2![]() ,
,
∴20=![]() FG(FG+6),整理得:FG2+6FG-40=0.
FG(FG+6),整理得:FG2+6FG-40=0.
解得:FG=4,FG=-10(舍去).
∵DF=GE=2![]() ,AF=10,
,AF=10,
∴AD=![]() .
.
∵GH⊥DC,AD⊥DC,
∴GH∥AD.
∴△FGH∽△FAD.
∴![]() ,即
,即![]() .
.
∴GH=![]() .
.
∴BE=AD-GH=4![]() -
-![]() =
=![]() ,故④正确.
,故④正确.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.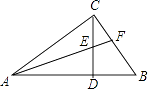
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.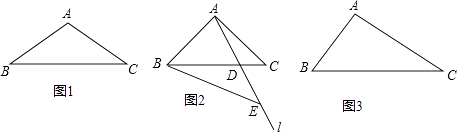
(1)若AB=AC,点E在AD延长线上.
当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=°,
∠BEA=°;
(2)如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
(3)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2. 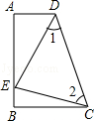
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B(A点在B点的左侧)与
轴交于A、B(A点在B点的左侧)与![]() 轴交于点C.
轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若![]() 时,求点P的横坐标;
时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥![]() 轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=
轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=![]() ,连接KB并延长交抛物线于点Q,求PQ的长.
,连接KB并延长交抛物线于点Q,求PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com