
【题目】钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.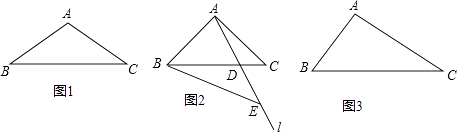
(1)若AB=AC,点E在AD延长线上.
当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=°,
∠BEA=°;
(2)如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
(3)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.
【答案】
(1)60;30
(2)
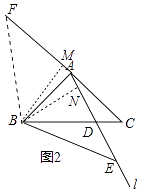
解:如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
∵AB=AC,
∴∠ABC=∠C=α,
∴∠MAB=2α,∵∠BAN=2α,
∴∠BAM=∠BAN,
∴BM=BN,
在Rt△BMF和Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE.
∴∠BEA=∠F,
∵BF=BC,
∴∠F=∠C=α,
∴∠BEA=α
(3)
解:结论:∠BAE=α+β.理由如下,
如图3中,连接EC,
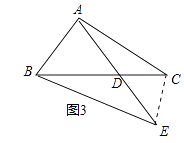
∵∠ACD=∠BED=α,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠ADB=∠CDE,
,∵∠ADB=∠CDE,
∴△ADB∽△CDE,
∴∠BAD=∠DCE,
∠ABD=∠DEC=β,
∵BC=BE,
∴∠BCE=∠BEC,
∴∠BAE=∠BEC=∠BEA+∠DEC=α+β
【解析】解:(1)补全图1,如图所示.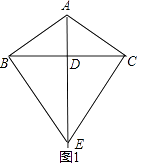
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEC=60°,∠BEA=30°
故答案为60,30.
(1)只要证明AE⊥BC,△BCE是等边三角形即可解决问题.(2)如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.
只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.(3)如图3中,连接EC,由△ADC∽△BDE,推出 ![]() =
= ![]() ,推出
,推出 ![]() =
= ![]() ,由∠ADB=∠CDE,推出△ADB∽△CDE,推出∠BAD=∠DCE,∠ABD=∠DEC=β,由BC=BE,推出∠BCE=∠BEC,推出∠BAE=∠BEC=∠BEA+∠DEC=α+β.
,由∠ADB=∠CDE,推出△ADB∽△CDE,推出∠BAD=∠DCE,∠ABD=∠DEC=β,由BC=BE,推出∠BCE=∠BEC,推出∠BAE=∠BEC=∠BEA+∠DEC=α+β.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形. 
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.给出以下结论: ①DG=DF; ②四边形EFDG是菱形; ③![]() ;
;
④当![]() 时,BE的长为
时,BE的长为![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
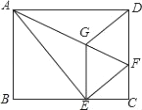
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com