


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| OB |
| OA |
| OB |
| OA |
| 1 |
| 2 |
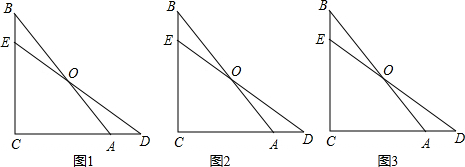
查看答案和解析>>
科目:初中数学 来源: 题型:
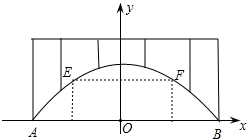 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-| 1 |
| 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
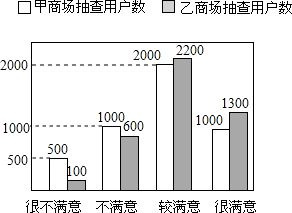 在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.
在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.查看答案和解析>>
科目:初中数学 来源: 题型:
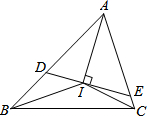 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com