
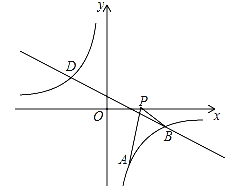
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象的交点为点B、D,且B(3,﹣1),求:
的图象的交点为点B、D,且B(3,﹣1),求:
(1)求反比例函数的解析式;
(2)求点D坐标,并直接写出y1>y2时x的取值范围;
(3)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
【答案】(1)![]() ;(2)D(-2,
;(2)D(-2,![]() ),-2<x<0,或x>3;(3)P(4,0).
),-2<x<0,或x>3;(3)P(4,0).
【解析】试题分析:(1)把点B(3,﹣1)带入反比例函数![]() 中,即可求得k的值;
中,即可求得k的值;
(2)联立直线和反比例函数的解析式构成方程组,化简为一个一元二次方程,解方程即可得到点D坐标,观察图象可得相应x的取值范围;
(3)把A(1,a)是反比例函数![]() 的解析式,求得a的值,可得点A坐标,用待定系数法求得直线AB的解析式,令y=0,解得x的值,即可求得点P的坐标.
的解析式,求得a的值,可得点A坐标,用待定系数法求得直线AB的解析式,令y=0,解得x的值,即可求得点P的坐标.
试题解析:(1)∵B(3,﹣1)在反比例函数![]() 的图象上,
的图象上,
∴-1=![]() ,
,
∴m=-3,
∴反比例函数的解析式为![]() ;
;
(2)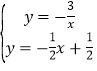 ,
,
∴![]() =
=![]() ,
,
x2-x-6=0,
(x-3)(x+2)=0,
x1=3,x2=-2,
当x=-2时,y=![]() ,
,
∴D(-2,![]() );
);
y1>y2时x的取值范围是-2<x<0或x>![]() ;
;
(3)∵A(1,a)是反比例函数![]() 的图象上一点,
的图象上一点,
∴a=-3,
∴A(1,-3),
设直线AB为y=kx+b,
![]() ,
,
∴![]() ,
,
∴直线AB为y=x-4,
令y=0,则x=4,
∴P(4,0)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
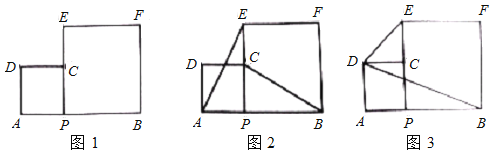
【题目】已知,AB=18,动点P从点A出发,以每秒1个单位的速度向点B运动,分别以AP、BP为边在AB的同侧作正方形。设点P的运动时间为t.
(1)如图1,若两个正方形的面积之和![]() ,
,![]() 当时,求出
当时,求出![]() 的大小;
的大小;
(2)如图2,当![]() 取不同值时,判断直线
取不同值时,判断直线![]() 和
和![]() 的位置关系,说明理由;
的位置关系,说明理由;
(3)如图3,用![]() 表示出四边形
表示出四边形![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
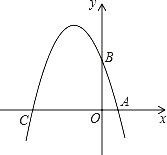
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,![]() ),B(-1,2)是一次函数y=kx+b与反比例函数y=
),B(-1,2)是一次函数y=kx+b与反比例函数y=![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连结PC、PD,若△PCA和△PDB面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备用体育用品 | 篮球 | 排球 | 羽毛球拍 |
单位(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?若能,求出篮球、排球、羽毛球拍各购买多少件;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
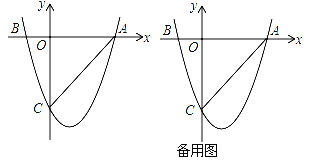
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣3)
(1)求该二次函数的解析式;
(2)设E是y轴右侧抛物线上异于点A的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH,则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)设P点是x轴下方的抛物线上的一个动点,连接PA、PC,求△PAC面积的取值范围,若△PAC面积为整数时,这样的△PAC有几个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校公布了该校反映各年级学生体育达标情况的两张统计图,该校七、八、九三个年级共有学生800人。甲,乙,丙三个同学看了这两张统计图后,甲说:“七年级的体育达标率最高.”乙说:“八年级共有学生264人。”丙说:“九年级的体育达标率最高。”甲、乙、丙三个同学中,说法正确的是_____________。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图正方形
中,如图正方形![]() 的顶点
的顶点![]() ,
,![]() 坐标分别为
坐标分别为![]() ,
,![]() ,点
,点![]() ,
,![]() 坐标分别为
坐标分别为![]() ,
,![]() ,且
,且![]() ,以
,以![]() 为边作正方形
为边作正方形![]() .设正方形
.设正方形![]() 与正方形
与正方形![]() 重叠部分面积为
重叠部分面积为![]() .
.

(1)①当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为______;②当点
的值为______;②当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为______.
的值为______.
(2)请用含![]() 的式子表示
的式子表示![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com