
【题目】如图,已知⊙O是以AB为直径的△ABC的外接圆,过点A作⊙O的切线交OC的延长线于点D,交BC的延长线于点E.
(1)求证:∠DAC=∠DCE;
(2)若AB=2,sin∠D=![]() ,求AE的长.
,求AE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由切线的性质可知∠DAB=90°,由直角所对的圆周为90°可知∠ACB=90°,根据同角的余角相等可知∠DAC=∠B,然后由等腰三角形的性质可知∠B=∠OCB,由对顶角的性质可知∠DCE=∠OCB,故此可知∠DAC=∠DCE;
(2)题意可知AO=1,OD=3,DC=2,由勾股定理可知AD=![]() ,由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA,故此可得到DC2=DEAD,故此可求得DE=
,由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA,故此可得到DC2=DEAD,故此可求得DE=![]() ,于是可求得AE=
,于是可求得AE=![]() .
.
试题解析:(1)∵AD是圆O的切线,∴∠DAB=90°.
∵AB是圆O的直径,∴∠ACB=90°.
∵∠DAC+∠CAB=90°,∠CAB+∠ABC=90°,∴∠DAC=∠B.
∵OC=OB,∴∠B=∠OCB.
又∵∠DCE=∠OCB,∴∠DAC=∠DCE.
(2)∵AB=2,∴AO=1.
∵sin∠D=![]() ,∴OD=3,DC=2.
,∴OD=3,DC=2.
在Rt△DAO中,由勾股定理得AD=![]() =
=![]() .
.
∵∠DAC=∠DCE,∠D=∠D,∴△DEC∽△DCA,∴![]() ,即
,即![]() .
.
解得:DE=![]() ,∴AE=AD﹣DE=
,∴AE=AD﹣DE=![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
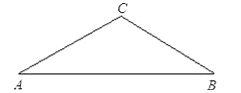
【题目】如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌商品,按标价九折出售,仍可获得20%的利润,若该商品标价为28元,则商品的进价为( )
A.21元
B.19.8元
C.22.4元
D.25.2元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为( )
A.312×104
B.0.312×107
C.3.12×106
D.3.12×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明(在括号中填写推理理由) 如图,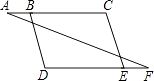
已知∠A=∠F,∠C=∠D,求证:BD∥CE.
证明:因为∠A=∠F,
所以AC∥DF(),
所以∠C+∠=180°().
因为∠C=∠D,
所以∠D+∠=180°(),
所以BD∥CE().
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下列各式因式分解:
①2m(a-b)-3n(b-a) ② (2a+b)2 -(a+2b)2
⑵计算:
① ( ![]() x2y-
x2y-![]() xy2-
xy2-![]() y3)(-4xy2) ② (a+2b-3c)(a-2b+3c)
y3)(-4xy2) ② (a+2b-3c)(a-2b+3c)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com