
【题目】如图,已知一次函数y=![]() x3与反比例函数y=
x3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为___,k的值为___;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y2时,请直接写出自变量x的取值范围。
的图象,当y2时,请直接写出自变量x的取值范围。
【答案】(1)n=3,k=12;(2)(4+![]() ,3);(3)x6或x>0.
,3);(3)x6或x>0.
【解析】
(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=
x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比例函数的性质即可得到当y≥-2时,自变量x的取值范围.
(1)把点A(4,n)代入一次函数y=![]() x3,可得n=
x3,可得n=![]() ×43=3;
×43=3;
把点A(4,3)代入反比例函数y=![]() ,可得3=
,可得3=![]() ,
,
解得k=12.
(2)∵一次函数y=![]() x3与x轴相交于点B,
x3与x轴相交于点B,
∴![]() x3=0,
x3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,

过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OEOB=42=2,
在Rt△ABE中,
AB=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3).
,3).
(3)当y=2时,2=![]() ,解得x=6.
,解得x=6.
故当y2时,自变量x的取值范围是x6或x>0.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
(1)用代数式表示这两个篮球场的占地面积.
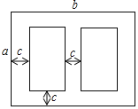
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
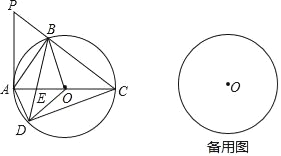
【题目】如图,在△ABC中,∠ABC=90°,⊙O是△ABC外接圆,点D是圆上一点,点D、B分别在AC两侧,且BD=BC,连接AD、BD、OD、CD,延长CB到点P,使∠APB=∠DCB.
(1)求证:AP为⊙O的切线;
(2)若⊙O的半径为1,当△OED是直角三角形时,求△ABC的面积;
(3)若△BOE、△DOE、△AED的面积分别为a、b、c,试探究a、b、c之间的等量关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体A,如图所示.
(1)请画出这个几何体A的三视图.


(2)若将此几何体A的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
(3)若现在你的手头还有一些相同的小正方体可添放在几何体A上,要保持主视图和左视图不变,则最多可以添加_______个小正方体.
(4)若另一个几何体B与几何体A的主视图和左视图相同,而小正方体个数则比几何体A多1个,请画出几何体B的俯视图的可能情况(画出你认为正确的2种不同情形即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°.∠BOC=30°,OM平分∠AOC,ON平分∠BOC.

(1)求∠MON的度数;
(2)若∠BOC=60°,其他条件不变,则∠MON= ;
(3)若∠AOB=α,其他条件不变,求∠MON的度数;
(4)从上面的结果能看出什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O是AB上的一点,从O点引出射线OC、OE、OD,其中OE平分∠BOC.
(1)如图1,若∠COD是直角,∠DOE=15°,求∠AOE的度数;
(2)如图1,若∠AOC=∠BOD,∠DOE=15°,求∠AOE的度数;
(3)将图1中的∠COD (∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=![]() , ∠DOE=
, ∠DOE=![]() ,请猜想
,请猜想![]() 与
与![]() 之间存在什么样的数量关系,写出你的结论,并说明理由.
之间存在什么样的数量关系,写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们环保意识的增强,越来越多的人选择低碳出行,各种品牌的山地自行车相继投放市场.顺风车行五月份![]() 型车的销售总利润为
型车的销售总利润为![]() 元,
元,![]() 型车的销售总利润为
型车的销售总利润为![]() 元.且
元.且![]() 型车的销售数量是
型车的销售数量是![]() 型车的
型车的![]() 倍,已知销售
倍,已知销售![]() 型车比
型车比![]() 型车每辆可多获利
型车每辆可多获利![]() 元.
元.
(1)求每辆![]() 型车和
型车和![]() 型车的销售利润;
型车的销售利润;
(2)若该车行计划一次购进![]() 两种型号的自行车共
两种型号的自行车共![]() 台且全部售出,其中
台且全部售出,其中![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车的
型车的![]() 倍,则该车行购进
倍,则该车行购进![]() 型车、
型车、![]() 型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b-![]() <0的解集(直接写出答案).
<0的解集(直接写出答案).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com