
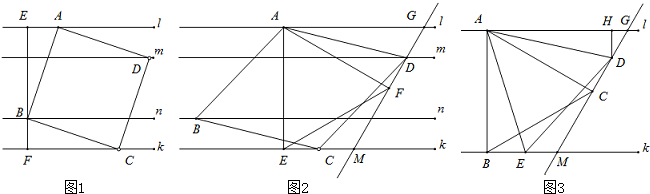
| BE2+AE2 |
| 32+12 |
| 10 |
| 10 |

| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
12+(
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |



 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
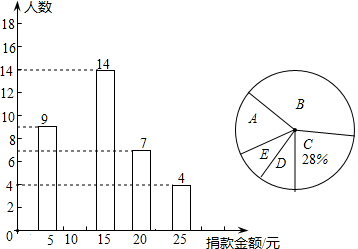 某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.
某学校九年级一班的全体同学长期帮助一名孤寡老人,2014年3月份为了达成老人的一个心愿,该班组织了一次捐款活动,捐款情况的部分统计如图.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
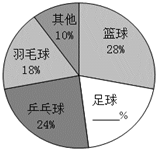 某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题:
某校课外活动小组为了了解学生最喜欢的球类运动的情况,随机抽查了该校学生,调查数据整理如图,请根据扇形统计图解答以下问题:| 球类 | 篮球 | 足球 | 乒乓球 | 羽毛球 | 其他 |
| 人数(人) | 14 | 12 | 9 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com