
【题目】如图,在锐角△ABC中,AD是BC边上的高.∠BAF=∠CAG=90°,且AB=AF=AC=AG.连接FG,交DA的延长线于点E,连接BG,CF.下列结论:①∠FAG+∠BAC=180°;②BG=CF;③BG⊥CF;④∠EAF=∠ABC.其中一定正确的个数是( )
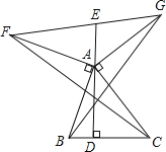
A.4个B.3个C.2个D.1个
【答案】A
【解析】
利用周角及∠BAF=∠CAG=90°,可推得①正确;易证得△CAF≌△GAB(SAS),从而推得②正确;利用△CAF≌△GAB及三角形内角和与对顶角,可判断③正确;利用等腰三角形三线合一性质及互余关系可推得④正确.
解:∵∠BAF=∠CAG=90°,
∴∠FAG+∠BAC=360°-90°-90°=180°,故①正确;
∵∠BAF=∠CAG=90°
∴∠BAF+∠BAC=∠CAG+∠BAC,即∠CAF=∠GAB
又∵AB=AF=AC=AG,
∴△CAF≌△GAB(SAS),
∴BG=CF,故②正确;
∵△FAC≌△BAG
∴∠FCA=∠BGA
又∵BC与AG所交的对顶角相等
∴BG与FC所交角等于∠GAC,即等于90°
∴BG⊥CF,故③正确;
∵AB=AC,AD⊥BC
∴∠BAD=∠CAD
∴∠EAF=∠CAG
∵∠EAF+∠BAD=∠ABC+∠BAD=90°
∴∠EAF=∠ABC,故④正确.
故选:A.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )

A. 6 B. 4![]() C. 3
C. 3![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.
(1)求证:四边形EGFH是菱形;
(2)若AB=4,且BA、CD延长后相交所成的锐角是60°,求四边形EGFH的面积.
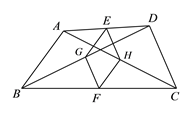
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一次函数y=kx+b的图像交x轴正半轴于点A、y轴正半轴于点B,且OA=OB=1.以线段AB为边在第一象限作正方形ABCD,点D在反比例函数y=![]() 图像上.
图像上.
(1)求一次函数的关系式,并判断点C是否在反比例函数y=![]() 图像上;
图像上;
(2)在直线AB上找一点P,使PC+PD的值最小,并求出点P的坐标.
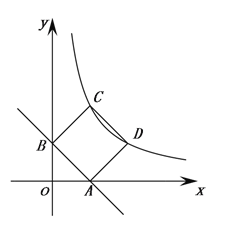
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元;如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元。
(1)求每个甲种规格的排球和每个已汇总规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3080元,那么该学校至多能购买多少个乙种规格的足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为一电视塔,AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上,被一个人工湖隔开),某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°;沿着山坡向上行走40m到达C处,此时测得塔顶M的仰角为30°,请求出电视塔MN的高度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本价为20元/千克,经市场调查,每天销售量y(千克)与销售单价x(元/千克)之间的关系如图所示,规定每千克售价不能低于30元,且不高于80元.
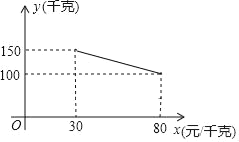
(1)求y与x之间的函数关系式,并直接写出自变量x的取值范围.
(2)每天销售量为135千克时,销售单价为 元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=
x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=![]() x+3上,若N点在第二象限内,则tan∠AON的值为( )
x+3上,若N点在第二象限内,则tan∠AON的值为( )
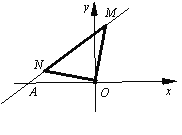
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com