
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于![]() PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织初中2000名学生游览“黄河口生态旅游区”,并以此开展“黄河文化”知识竞赛活动,现从中随机抽取若干名学生的得分![]() 满分100分,成绩均为正数
满分100分,成绩均为正数![]() 进行统计,整理出下列竞赛成绩统计表和扇形统计图
进行统计,整理出下列竞赛成绩统计表和扇形统计图![]() 均不完整
均不完整![]() .
.
成绩统计表

如果成绩在90分以上![]() 含90分
含90分![]() 可获得一等奖;70分以上
可获得一等奖;70分以上![]() 含70分
含70分![]() ,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
,90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
![]() 本次活动共随机抽取了多少名学生?
本次活动共随机抽取了多少名学生?
![]() 估计本次活动获得二等奖的学生有多少名?
估计本次活动获得二等奖的学生有多少名?
![]() 绘制频数分布直方图.
绘制频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为16,点D是BC边上一点,且BD= ![]() BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() (a>0,a为常数)和y=
(a>0,a为常数)和y= ![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y= ![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= ![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= ![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y= ![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
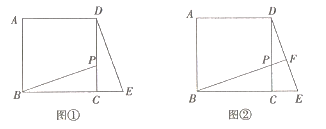
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com