
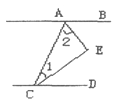
【题目】如图,已知AB∥CD,CE、AE分别平分![]() 、
、![]() ,则
,则![]() = ( )
= ( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】
由AB∥CD,根据两直线平行,同旁内角互补,可得∠BAC+∠ACD=180°,又由CE、AE分别平分∠ACD、∠CAB,可得![]() ,
,![]() ,则可求得∠1+∠2的度数.
,则可求得∠1+∠2的度数.
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵CE、AE分别平分∠ACD、∠CAB,
∴![]() ,
,![]() ,
,
∴![]() .
.
故选B.
【考点精析】通过灵活运用平行线的性质和三角形的内角和外角,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】端午节前夕,某校为学生购买了A、B两种品牌的粽子共400个,已知B品牌粽子的单价比A品牌粽子的单价的2倍少6元.
(1)当买A品牌100个,B品牌粽子300个时,学校所花费用为4500元.求A、B两种品牌粽子各自的单价;
(2)在两种品牌粽子单价不变的情况下,由于资金临时出现状况,所花费用不超过4000元,问至少买A品牌粽子多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C、D在坐标轴上,直线AB与直线CD:y=2x+2相交于点E(a,﹣3),连接BC,其中B(0,﹣5). 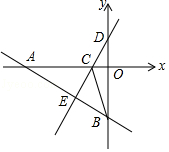
(1)求直线AB的解析式;
(2)求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在去年购买A,B两种足球,费用分别为2400元和2000元, 其中A种足球数量是B种足球数量的2倍,B种足球单价比A种足球单价多80元/个.
(1)求A,B两种足球的单价;
(2)由于该校今年被定为“足球特色校”,学校决定再次购买A,B两种足球共18个,且本次购买B种足球的数量不少于A种足球数量的2倍,若单价不变,则本次如何购买才能使费用W最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连接DE,CF.
BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菏泽牡丹机场位于菏泽市定陶区孟海镇西北,距満泽市中心直线距离约20公里,飞行区指标为4C级,跑道长2600米,菏泽机场性质为国内支线机场,计划2019年10月1日建成通航,预计机场年旅客吞吐量900000人次.数据900000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4 ![]() ,则四边形AECD的周长为( )
,则四边形AECD的周长为( ) 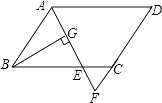
A.20
B.21
C.22
D.23
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com