
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处. 
(1)求AD的长;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?
【答案】
(1)解:由折叠可得,CE=CB=AO=10,而CO=AB=8,
∴OE=6,
∴AE=10﹣6=4,
设AD=x,则DB=DE=8﹣x,
Rt△ADE中,AD2+AE2=DE2,
∴x2+42=(8﹣x)2,
解得x=3,
∴AD=3;
(2)解:∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE,
由(1)可得,AD=3,AE=4,DE=5,
∵CQ=t,EP=2t,
∴PC=10﹣2t,
① 当∠PQC=∠DAE=90°时,△ADE∽△QPC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() ;
;
②当∠QPC=∠DAE=90°时,△ADE∽△PQC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
综上所述,当t= ![]() 或
或 ![]() 时,以P、Q、C为顶点的三角形与△ADE相似.
时,以P、Q、C为顶点的三角形与△ADE相似.

【解析】(1)先设AD=x,则DB=DE=8﹣x,在Rt△ADE中,根据勾股定理可得AD2+AE2=DE2 , 据此列出方程x2+42=(8﹣x)2 , 求得x=3,进而得到AD=3;(2)分两种情况进行讨论:①当∠PQC=∠DAE=90°时,△ADE∽△QPC,②当∠QPC=∠DAE=90°时,△ADE∽△PQC,分别根据相似三角形的性质,得出关于t的方程,求得t的值.
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
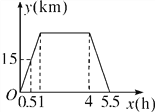
【题目】周末,小李从家里出发骑车到少年宫学习绘画,学完后立即回家,他离家的距离y(km)与时间x(h)之间的函数关系如图所示,有下列结论:①他家离少年宫30km;②他在少年宫一共停留了3h;③他返回家时,离家的距离y(km)与时间x(h)之间的函数表达式是y=-20x+110;④当他离家的距离y=10时,时间x=![]() .其中正确的是________(填序号).
.其中正确的是________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( ) 
A.6
B.6.25
C.6.5
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数按要求分类:
![]()
负整数集合:{____________________}
正分数集合:{____________________}
负分数集合:{____________________}
整数集合:{_______________________}
负有理数集合:{_______________________}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度. 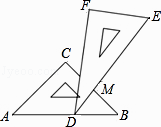
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,﹣1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com