
7.如图,D是等边三角形ABC内一点,且DB=DA,BP=AB,∠DBP=∠DBC,求∠P的度数.

根据等边三角形的性质就可以得出△ADC≌△BDC,就可以求出∠ACD=∠BCD=30°,再证明△BDP≌△BDC就可以得出∠P=∠BCD,从而得出结论.
【解析】
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
在△ADC和△BDC中,
AC=BC,
AD=BD,
CD=CD
∴△ADC≌△BDC(SSS),
∴∠ACD=∠BCD.
∵∠ACD+∠BCD=∠ACD=60°,
∴∠BCD=30°.
∵BP=AB,
∴BP=BC.
在△BDP和△BDC中,
BP=BC,
∠DBP=∠DBC,
BD=BD。
∴△BDP≌△BDC(SAS),
∴∠P=∠BCD,
∴∠P=30°.
答:∠P=30°.
题目来源:初中同步测控优化设计八年级数学上册人教版 > 13.3.2等边三角形


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
学前温故
1.等腰三角形是轴对称图形,它的对称轴是:_________(答案不唯一);
2.等腰三角形的_________,_________,__________相互重合。
查看答案和解析>>
科目:初中数学 来源: 题型:
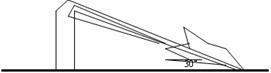
A.10m B.15m
C.25m D.30m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com