
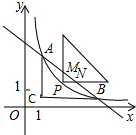
 如图,已知反比例函数y=
如图,已知反比例函数y=| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 1 |
| 2 |
| 5 |
| 2 |
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
| 4 |
| a |
| 1 |
| 2 |
| 2 |
| x |
| 2 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| a |
| 4 |
| a |
| 4 |
| a |
| 2 |
| a |
| 4 |
| a |
| MN |
| AB |
| NP |
| BC |
| 4 |
| a |


科目:初中数学 来源: 题型:
 调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为
调查机构对某地区1000名20~30岁年龄段观众周五综艺节目的收视选择进行了调查,相关统计图如下,请根据图中信息,估计该地区20000名20~30岁年龄段观众选择观看《最强大脑》的人数约为查看答案和解析>>
科目:初中数学 来源: 题型:
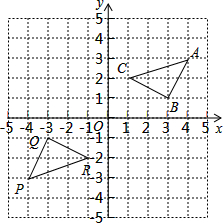 如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?
如图,三角形PQR是三角形ABC经过某种变换后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系,如果三角形ABC中任意一点M的坐标为(a,b),那么它的对应点N的坐标是什么?查看答案和解析>>
科目:初中数学 来源: 题型:
 张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由.
张华同学家要建一个长方形的养鸡场,鸡场的一边靠墙(墙长为25米),另三边用长40米的竹篱笆围成.问长方形的鸡场的面积能否达到128m2?如果能,AB的长是多少米?如果不能,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD.
如图,在⊙O中,点P为直径BA延长线上一点,直线PD切⊙O于点D,过点B作BH⊥PD,垂足为H,BH交⊙O于点C,连接BD. |
| AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com