
����Ŀ����֪����ʽ3x6��2x2��4�ij�����Ϊa������Ϊb��
��1����a��b�ֱ��Ӧ�����ϵĵ�A����B����ֱ��д��a���� ����b���� ��������������ȷ����A����B��λ�ã�
��2���ڣ�1���������£���P��ÿ��2����λ���ȵ��ٶȴӵ�A��B�˶����˶�ʱ��Ϊt�룺
����PA��PB��6����t��ֵ����д����ʱ��P����ʾ������
������P�ӵ�A�����������B��������ͬ���ٶȷ��ص�A���ڷ��ع����У���OP��3ʱ��tΪ��ֵ��
![]()
���𰸡���1����4��6����2����4����![]()
��������
��1�����ݶ���ʽ�ij�����������Ķ���ֱ����a��b��ֵ��Ȼ���������ϱ�ʾ���ɣ�
��2���ٸ���PA��PB��6�г�����t�ķ��̣��ⷽ�����t��ֵ�������õ���P����ʾ���������ڷ��ع����У���OP��3ʱ�������������������P��ԭ���ұߣ�������P��ԭ����ߣ��ֱ������P�˶���·�̣��ٳ����ٶȼ��ɣ�
��1���߶���ʽ3x6��2x2��4�ij�����Ϊa������Ϊb��
��a����4��b��6��
��ͼ��ʾ��
![]()
�ʴ�Ϊ��4��6��
��2���١�PA��2t��AB��6������4����10��
��PB��AB��PA��10��2t��
��PA��PB��6��
��2t����10��2t����6�����t��4��
��ʱ��P����ʾ����Ϊ��4+2t����4+2��4��4��
���ڷ��ع����У���OP��3ʱ�������������
���������P��ԭ���ұߣ���ôAB+BP��10+��6��3����13��t��![]() ��
��
���������P��ԭ����ߣ���ôAB+BP��10+��6+3����19��t��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����֪DE��AC��BF��AC������ֱ���E��F��AE=CF��DC��AB��
��1����֤����DE=BF��
��2������DF��BE������DF��BE�Ĺ�ϵ����֤����IJ������ȷ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��4��0����B��3��3������AO��ABΪ����ƽ���ı���OABC����C��ķ����������Ľ���ʽΪ �� 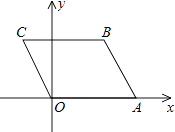
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF��AD,��1=��2,��BAC=70���������AGD�Ĺ�����д������
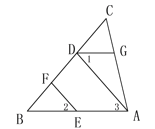
�⣺��EF��AD
�� =��3 (��ֱ��ƽ�У�ͬλ�����)
�֡ߡ�1=��2
���1=��3 (__________________)
�� ��DG (__________________________)
���BAC+______=180��(_________________________)
�ߡ�BAC=70��
���AGD=_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A=60�㣬��D��BC�ߵ��е㣬DE��BC����ABC�Ľ�ƽ����BF��DE�ڡ�ABC��һ��P������PC��
��1������ACP=24�㣬���ABP�Ķ�����
��2������ACP=m�㣬��ABP=n�㣬��ֱ��д��m��n����Ĺ�ϵʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���BAC��90����BE����ABC�Ľ�ƽ���ߣ�ED��BC�ڵ�D������AD.
(1)����д��ͼ�����еĵ��������Σ�
(2)��BC��10����AB��AE�ij���
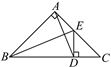
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֤������ͼ����֪AD��BC��EF��BC����1=��2.
��֤: DG��BA.
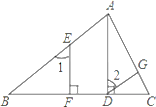
֤������AD��BC,EF��BC ( ��֪ )
���EFB=90��,��ADB=90��(_______________________ )
���EFB=��ADB ( �������� )
��EF��AD ( _________________________________ )
���1=��BAD (________________________________________)
���ߡ�1=��2 ( ��֪)
�� ������������
��DG��BA. (__________________________________)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
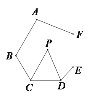
����Ŀ����ͼ����������ABCDEF�У���A����B����E����F������CP��DP�ֱ�ƽ�֡�BCD����CDE�����P�Ķ����ǣ�������
A. ![]() ����180��B. 180�㣭
����180��B. 180�㣭![]() C.
C. ![]() D. 360�㣭
D. 360�㣭![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����۲죩����![]() �Ľ���
�Ľ���![]() �Ľ���
�Ľ���![]() ��
��
![]() �Ľ���
�Ľ���![]() �Ľ���
�Ľ���![]()
�����֣���������Ķ��ش����⣺
��1��![]() �Ľ�Ϊ_______��
�Ľ�Ϊ_______��
��2������![]() �ķ���
�ķ���![]() �Ľ�Ϊ_______(�ú�
�Ľ�Ϊ_______(�ú�![]() �Ĵ���ʽ��ʾ)�������á����̵Ľ�ĸ����֤��
�Ĵ���ʽ��ʾ)�������á����̵Ľ�ĸ����֤��
����ȣ�
��3������![]() �ķ���
�ķ���![]() �Ľ�Ϊ_________(�ú�
�Ľ�Ϊ_________(�ú�![]() �Ĵ���ʽ��ʾ)��
�Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com