
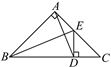
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,BE是△ABC的角平分线,ED⊥BC于点D,连接AD.
(1)请你写出图中所有的等腰三角形;
(2)若BC=10,求AB+AE的长.
【答案】(1)见解析;(2) AB+AE=10.
【解析】
(1)如图,根据△ABC是等腰直角三角形可知∠8=45°,由ED⊥BC可知∠7=∠8=45°,由此得到△DCE为等腰三角形;由角平分线的性质可知AE=DE,由此得到△AED为等腰三角形;同理可得△ABD为等腰三角形;
(2)由于△AED为等腰三角形,△ABD为等腰三角形,利用等腰三角形的性质即可证明AB+AE=BD+CD=BC,然后就可以求出AB+AE的长.
(1)如图,∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠C=45°.
又∵ED⊥BC,
∴∠EDC=90°,
∴∠7=∠C=45°,
∴DE=DC,

故△DCE为等腰直角三角形.
∵BE是△ABC的角平分线,∠BAC=∠BDE=90°,
∴AE=DE,
∴△ADE为等腰三角形.
∵BE是△ABC的角平分线,
∴∠1=∠2.
又∵∠BAE=∠BDE=90°,BE=BE,
∴△ABE≌△DBE,
∴AB=DB,
∴△ABD为等腰三角形.
故图中所有的等腰三角形为△ABC,△DCE,△ADE,△ABD,共4个.
(2)由(1)可知△ADE为等腰三角形,△ABD为等腰三角形,△DCE为等腰三角形,故AB=DB,AE=DE=DC,∴AB+AE=DB+DC=BC=10.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )

A. 2cm B. 4cm C. 2![]() cm D. 4
cm D. 4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
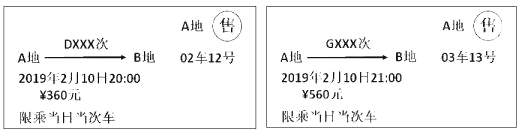
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式3x6﹣2x2﹣4的常数项为a,次数为b.
(1)设a与b分别对应数轴上的点A、点B,请直接写出a= ,b= ,并在数轴上确定点A、点B的位置;
(2)在(1)的条件下,点P以每秒2个单位长度的速度从点A向B运动,运动时间为t秒:
①若PA﹣PB=6,求t的值,并写出此时点P所表示的数;
②若点P从点A出发,到达点B后再以相同的速度返回点A,在返回过程中,求当OP=3时,t为何值?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
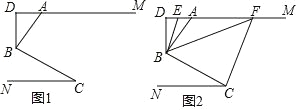
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
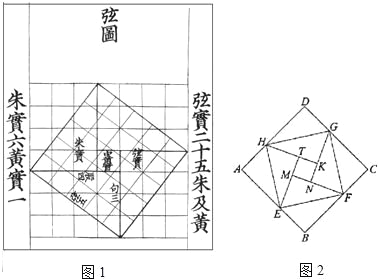
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com