
����Ŀ�����������Ų�ͬ���ͻij�Ʊ������D������������ʾ��������G������������ʾ��������
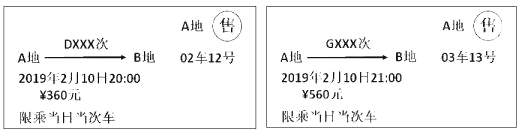
��1�����ݳ�Ʊ�е���Ϣ��գ�������ʻ������ ��������ʱ���� ����������ͬ��������ͬ������
��2����֪�ö���������ƽ���ٶȷֱ�Ϊ200km/h��300km/h���������������Ʊ��Ϣʱ��������ͬʱ�����յ㣬��A��B����֮��ľ��룻
��3���ڣ�2���������£��������ʲôʱ���������100km��
���𰸡���1����ͬ����ͬ����2��A��B����֮��ľ���Ϊ600km����3���ڣ�2���������£��ڸ�������1hʱ�������100km��
��������
��1�����ݳ�Ʊ�е���Ϣ���ɿ�������Ʊ���Ǵ�A�ص�B�أ����Է�����ͬ��������ʱ��ֱ���20��00��21��00�����Գ���ʱ�̲�ͬ��
��2������A��B����֮��ľ���Ϊs��������ͬʱ�����յ㣬���ǿ��з���![]() ��1��
��1��![]() ���ⷽ�̼���������ؾ��룻
���ⷽ�̼���������ؾ��룻
��3���������100km���Է���֮ǰ����֮���������Ϊ���ǣ���ͬʱҲҪ������������Ĵ����ԣ�
��1����Ʊ�е���Ϣ���ɿ�������Ʊ���Ǵ�A�ص�B�أ����Է�����ͬ����������ʱ��ֱ���20��00��21��00�����Գ���ʱ�̲�ͬ��
�ʴ�Ϊ����ͬ����ͬ��
��2����A��B����֮��ľ���Ϊs��
��������ɵ�![]() ��1��
��1��![]() ��
��
���s��600��
��A��B����֮��ľ���Ϊ600km��
��3�����ڸ�������tСʱ���������100km������ǰ���������������
��200��t+1����300t��100����� t��1��
��300t��200��t+1����100�����t��3��
�����ڣ�2���������£�600��300��2��
����������2Сʱ�ɵ���B�أ����Եڢ������������ʵ�ʣ�Ӧ����ȥ��
���ڣ�2���������£��ڸ�������1hʱ�������100km��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�DE��BC��BE��CD���ڵ�O��AO��DE��BC����N��M��������ʽ���д�����ǣ� ��
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C��90��������ACE����AE�۵��Ժ�C����������AB���ϵĵ�D����
��1������B��28��ʱ�����AEC�Ķ�����
��2����AC��6��AB��10ʱ��
�����߶�BC�ij���
�����߶�DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������㣺��������ʵ��a��b������a��0��������ab= ![]() ��
�� ![]() ����ʽ�ұ���ͨ���ļӷ����������������㣬����23=
����ʽ�ұ���ͨ���ļӷ����������������㣬����23= ![]() ��
�� ![]() =
= ![]() +
+ ![]() =1��
=1��
��1����2��3��ֵ��
��2����x2=1����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF��AD,��1=��2,��BAC=70���������AGD�Ĺ�����д������
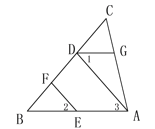
�⣺��EF��AD
�� =��3 (��ֱ��ƽ�У�ͬλ�����)
�֡ߡ�1=��2
���1=��3 (__________________)
�� ��DG (__________________________)
���BAC+______=180��(_________________________)
�ߡ�BAC=70��
���AGD=_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD��EF��CE��EF����2+��3=180����
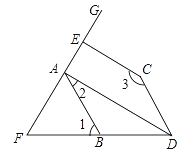
��1����˵����1=��BDC��
��2������1=70����DAƽ�֡�BDC�������FAB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
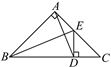
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���BAC��90����BE����ABC�Ľ�ƽ���ߣ�ED��BC�ڵ�D������AD.
(1)����д��ͼ�����еĵ��������Σ�
(2)��BC��10����AB��AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
��������һ���е���������Զ�����߶γ�Ϊ�����ε����ߡ�
�����ε����ߵ����ʣ������ε����ߵȷ������ε������
����ͼ1��AD��![]() ��BC���ϵ����ߣ���
��BC���ϵ����ߣ���![]() ��
��
���ɣ�![]() ��
��![]() ��
��
�����ȵ�ͬ�ߵ������������ȡ�
������̽����

����ͼ2��ͼ4�У�![]() �����Ϊa��
�����Ϊa��
��1����ͼ2���ӳ�![]() �ı�BC����D��ʹCD=BC������DA����
�ı�BC����D��ʹCD=BC������DA����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ���ú�a�Ĵ���ʽ��ʾ����
���ú�a�Ĵ���ʽ��ʾ����
��2����ͼ3���ӳ�![]() �ı�BC����D���ӳ���CA����E��ʹCD=BC��AE=CA������DE����
�ı�BC����D���ӳ���CA����E��ʹCD=BC��AE=CA������DE����![]() �����Ϊ
�����Ϊ![]() ����
����![]() _________���ú�a�Ĵ���ʽ��ʾ����
_________���ú�a�Ĵ���ʽ��ʾ����
��3����ͼ3�Ļ������ӳ�AB����F��ʹBF=AB������FD��FE���õ�![]() ����ͼ4��������Ӱ���ֵ����Ϊ
����ͼ4��������Ӱ���ֵ����Ϊ![]() ����
����![]() ________���ú�a�Ĵ���ʽ��ʾ��
________���ú�a�Ĵ���ʽ��ʾ��
��4����չ��Ӧ�ã�
��ͼ5����֪�ı���ABCD�������a;E,F,G,H�ֱ���AB��BC��CD���е㣬��ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC��AB��2��CD�DZ�AB�ĸ��ߣ�����E�ӵ�A��������ÿ��1����λ���ٶ�������AC�˶���ͬʱ������F�ӵ�C����������ͬ���ٶ�������CB�˶�����E���˶�ʱ��Ϊt��s����t��0����
��1��AE���� �����ú�t�Ĵ���ʽ��ʾ������BCD�Ĵ�С���� ���ȣ�
��2����E�ڱ�AC���˶�ʱ����֤����ADE�ա�CDF��
��3����E�ڱ�AC���˶�ʱ�����EDF�Ķ�����
��4������BE����CE��ADʱ��ֱ��д��t��ֵ�ʹ�ʱBE��Ӧ��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com