
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC��AB��2��CD�DZ�AB�ĸ��ߣ�����E�ӵ�A��������ÿ��1����λ���ٶ�������AC�˶���ͬʱ������F�ӵ�C����������ͬ���ٶ�������CB�˶�����E���˶�ʱ��Ϊt��s����t��0����
��1��AE���� �����ú�t�Ĵ���ʽ��ʾ������BCD�Ĵ�С���� ���ȣ�
��2����E�ڱ�AC���˶�ʱ����֤����ADE�ա�CDF��
��3����E�ڱ�AC���˶�ʱ�����EDF�Ķ�����
��4������BE����CE��ADʱ��ֱ��д��t��ֵ�ʹ�ʱBE��Ӧ��ֵ��

���𰸡���1��t��45����2�������������3��90������4��t��ֵΪ![]() ��1��
��1��![]() +1��BE=
+1��BE=![]() ��
��
��������
��1�����ݵ���ֱ�������ε����ʼ��ɽ�����⣻
��2������SAS����֤����ADE�ա�CDF��
��3���ɡ�ADE�ա�CDF�������Ƴ���ADE=��CDF���Ƴ���EDF=��ADC=90�㣻
��4�����������ηֱ���⼴�ɽ�����⣮
��1�������⣺AE=t��
��CA=CB����ACB=90�㣬CD��AB�����BCD=��ACD=45�㣮
�ʴ�Ϊ��t��45��
��2���ߡ�ACB=90�㣬CA=CB��CD��AB����CD=AD=BD�����A=��DCB=45�㣮
��AE=CF�����ADE�ա�CDF��SAS����
��3���ߵ�E�ڱ�AC���˶�ʱ����ADE�ա�CDF�����ADE=��CDF�����EDF=��ADC=90�㣮
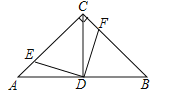
��4���ٵ���E��AC����ʱ����ͼ1����Rt��ACB�У��ߡ�ACB=90�㣬AC=CB��AB=2��CD��AB����CD=AD=DB=1��AC=BC![]() ��
��
��CE=CD=1����AE=AC��CE![]() 1����t
1����t![]() 1��
1��
��BC=![]() ����BE=
����BE=![]() =
=![]() =
=![]() ��
��
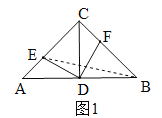
�ڵ���E��AC���ӳ�����ʱ����ͼ2��AE=AC+EC![]() 1����t
1����t![]() 1��
1��
��BC=![]() ����BE=
����BE=![]() =
=![]() =
=![]() ��
��
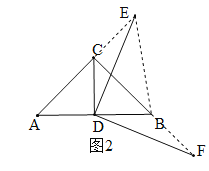
��������������������t��ֵΪ![]() 1��
1��![]() 1��BE=
1��BE=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ų�ͬ���ͻij�Ʊ������D������������ʾ��������G������������ʾ��������
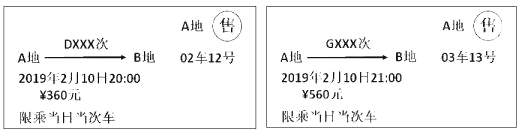
��1�����ݳ�Ʊ�е���Ϣ��գ�������ʻ������ ��������ʱ���� ����������ͬ��������ͬ������
��2����֪�ö���������ƽ���ٶȷֱ�Ϊ200km/h��300km/h���������������Ʊ��Ϣʱ��������ͬʱ�����յ㣬��A��B����֮��ľ��룻
��3���ڣ�2���������£��������ʲôʱ���������100km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABCD�У���BAD��ƽ���߽�ֱ��BC�ڵ�E����ֱ��DC�ڵ�F��
��1����ͼ1��֤��CE=CF��
��2������ABC=90�㣬G��EF���е㣨��ͼ2����ֱ��д����BDG�Ķ�����
��3������ABC=120�㣬FG��CE��FG=CE���ֱ�����DB��DG����ͼ3��������BDG�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
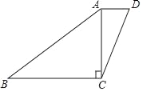
����Ŀ����ͼ��һ���ı���ֽƬABCD��AB��20��BC��16��CD��13��AD��5���Խ���AC��BC��
��1����AC�ij���
��2�����ı���ֽƬABCD�������
��3�������ı���ֽƬABCD��AC������ƴ��һ�����ı���ֽƬABCD�����ȵ������Σ�ֱ��д��ƴ�õ������θ��߸ߵij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�ļ����ڣ�
3.1415926����2.1��|��![]() |�� 0��
|�� 0�� ![]() �� -2.626626662����
�� -2.626626662����![]() ��
�� ![]() ��
��
�������ϣ�{ ��}
�������ϣ�{ ��}
���������ϣ�{ ��}
���������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8����M��AC���ϣ���N�ӵ�C����������CB��BA�˶�����Aֹͣ����P�ǵ�C����ֱ��MN�ĶԳƵ㣬����MP��NP������N���C��A�غ�ʱ����P�����C�غϣ���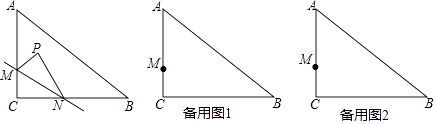
��1����CM=2��
���ֵ���N��CB�ϣ�MP��BCʱ����CN= �� MN=��
��2���ڣ�1���������£����P��AB�ߵľ������Сֵ���������ȡ�������Сֵʱ����P�˶�·�ߵij��Ƕ��٣����ο����ݣ�sin54��=cos36��� ![]() ��sin36��=cos54���
��sin36��=cos54��� ![]() �����������
�����������
��3����MC=a��a��2���������������䣬������ֻ����Ψһ�ĵ�P�����߶�AB��ʱ��ֱ��д��a��ȡֵ��Χ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��-15-[-1-��4-22��5��]
��2��-12019-��1-![]() ����|3-��-3��2|
����|3-��-3��2|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AB=AC=4��BC=5����D�DZ�AB���е㣬��E�DZ�AC���е㣬��P�DZ�BC�ϵĶ��㣬��DPE=��C����BP= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺
��1������8��+3+10+����2��
��2������2��������6��������![]() ��
��
��3������1��100��2+����2��3��4
��4��2��a��3b��+3��2b��3a��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com