
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合).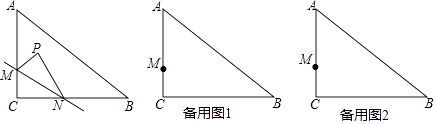
(1)若CM=2,
①又当点N在CB上,MP∥BC时,则CN= , MN=;
(2)在(1)的条件下,求点P到AB边的距离的最小值,并求出当取得这个最小值时,点P运动路线的长是多少?(参考数据:sin54°=cos36°≈ ![]() ,sin36°=cos54°≈
,sin36°=cos54°≈ ![]() ,结果保留π)
,结果保留π)
(3)设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围 .
【答案】
(1)2,2 ![]() ②又当MN∥AB时,求CN的长;解:当MN∥AB时,△MNC∽△ABC,∴
②又当MN∥AB时,求CN的长;解:当MN∥AB时,△MNC∽△ABC,∴ ![]() ,即
,即 ![]() ,∴CN=
,∴CN= ![]()
(2)解:P在M为圆心,CM为半径的圆周上运动,
作MT⊥AB于T,如图2所示:

则PT=MT﹣2,当MT最小时,P在线段MT上最小,
∵AB= ![]() =10,sinA=
=10,sinA= ![]() =
= ![]() =
= ![]() ,
,
∴MT= ![]() AM=
AM= ![]() (6﹣2)=
(6﹣2)= ![]() ,
,
∴PT= ![]() ﹣2=
﹣2= ![]() ,
,
即点P到AB边的距离的最小值为 ![]() ;
;
∵cos∠AMT=sinA= ![]() ,
,
∴∠AMT=36°,
∴∠CMT=180°﹣36°=144°,
∴点P运动路线的长= ![]() =
= ![]()
(3)a= ![]() 或3<a≤6
或3<a≤6
【解析】解:(1)①连接CP,如图1所示:
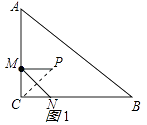
由对称的性质得:PM=CM=2,PC⊥MN,
∵MP∥BC,∠C=90°,
∴∠PMC=90°,
∴△PMC是等腰直角三角形,
∴∠PCM=45°,
∴∠PCN=90°﹣45°=45°,
∴∠CNM=45°,
∴△CMN是等腰直角三角形,
∴CN=CM=2,MN= ![]() CM=2
CM=2 ![]() ;
;
所以答案是:2,2 ![]() ;
;
⑶分情况:①当圆M与AB相切时,sinA= ![]() ,
,
解得:a= ![]() ;②当
;②当 ![]() <a≤3时,圆M与AB有2个交点;③当3<a≤6时,圆M与线段AB仅1个交点;
<a≤3时,圆M与AB有2个交点;③当3<a≤6时,圆M与线段AB仅1个交点;
综上所述:当a= ![]() 或3<a≤6时,圆M与线段AB有1个交点;
或3<a≤6时,圆M与线段AB有1个交点;
即当有且只能有唯一的点P落在线段AB上时,a的取值范围是a= ![]() 或3<a≤6;
或3<a≤6;
所以答案是:a= ![]() 或3<a≤6.
或3<a≤6.
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点,需要掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
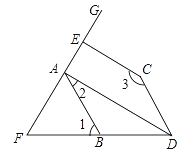
(1)请说明∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )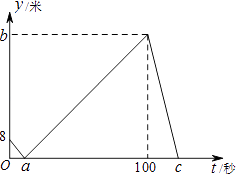
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,AB=2 ![]() ,AC是对角线,∠B=60°,点E在BC边上,点F在DC边上,且∠EAF=60°,AE与DC的延长线交于点M,AF与BC的延长线交于点N.
,AC是对角线,∠B=60°,点E在BC边上,点F在DC边上,且∠EAF=60°,AE与DC的延长线交于点M,AF与BC的延长线交于点N.
(1)如图1,若点E为BC边上的中点.
①求证:△ACM≌△ACN;
(2)如图2,若点E为BC边上的任意点(不与点B,C重合),请说明CMNC是一个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AB=2,CD是边AB的高线,动点E从点A出发,以每秒1个单位的速度沿射线AC运动;同时,动点F从点C出发,以相同的速度沿射线CB运动.设E的运动时间为t(s)(t>0).
(1)AE= (用含t的代数式表示),∠BCD的大小是 度;
(2)点E在边AC上运动时,求证:△ADE≌△CDF;
(3)点E在边AC上运动时,求∠EDF的度数;
(4)连结BE,当CE=AD时,直接写出t的值和此时BE对应的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的![]() 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x+y=7,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1). 
①以O为位似中心在第二象限作位似比为1:2变换,得到对应的△A1B1C1 , 画出△A1B1C1 , 并写出C1的坐标;
②以原点O为旋转中心,画出把△ABC顺时针旋转90°的图形△A2B2C2 , 并写出C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com