练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米，先到终点的人原地休息．已知甲先出发2秒．在跑步过程中，甲、乙两人的距离y（米）与乙出发的时间t（秒）之间的关系如图所示，给出以下结论：①a=8；②b=92；③c=123．其中正确的是（ ）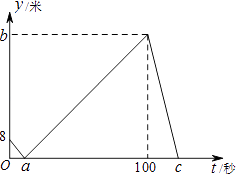

    A.①②③
    B.仅有①②
    C.仅有①③
    D.仅有②③

    【答案】A
    【解析】甲的速度为：8÷2=4（米/秒）；

    乙的速度为：500÷100=5（米/秒）；

    b=5×100﹣4×（100+2）=92（米）；

    5a﹣4×（a+2）=0，

    解得a=8，

    c=100+92÷4=123（秒），

    ∴正确的有①②③．

    故答案为：A．

    本题是一道一次函数的综合试题，考查了路程=速度×时间的运用，追击问题的运用，由图象可以看出甲2秒跑了8米可以求出甲的速度为4米/秒，b是表示乙跑到终点时甲乙的距离，c表示乙出发后甲到达终点的时间．根据总路程÷速度-甲先走的时间即是c的值，即可得到所求结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线Y=ax2+bx一3与X轴相交于A(一1，0)，B(3，0)，P为抛物线上第四象限上的点．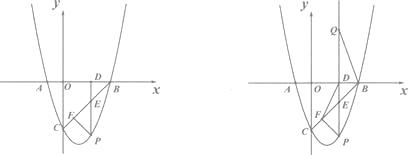

    （1）求该抛物线的函数关系式．
    （2）过点P作PD⊥X轴于点D，PD交BC于点E，当线段PE的长度最大时，求点P的坐标．
    （3）当线段PE的长度最大时，作PF ⊥BC于点F，连结DF．在射线PD上有一点Q，满足∠PQB=∠DFB，问在坐标轴上是否存在一点R，使得S△RBE=S△QBE；如果存在，直接写出R点的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 1，AM∥CN，点 B 为平面内一点，AB⊥BC 于 B，过 B 作 BD⊥ AM．

    （1）求证：∠ABD=∠C；

    （2）如图 2，在（1）问的条件下，分别作∠ABD、∠DBC 的平分线交 DM 于 E、F，若∠BFC=1.5∠ABF，∠FCB=2.5∠BCN，

    ①求证：∠ABF=∠AFB；

    ②求∠CBE 的度数．

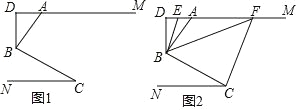
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小晶设计的“作互相垂直的两条直线”的尺规作图过程．

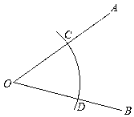
    作法：如图，

    ①在平面内任选一点O，作射线OA，OB；

    ②以O为圆心，以任意长为半径作弧，分别交OA于点C，交OB于点D；

    ③分别以C，D为圆心，以大于CD的同样长为半径作弧，两弧交于∠AOB内部一点P；

    ④连接CP、PD；

    ⑤作直线OP，作直线CD，两直线相交于点E；则直线CD与OP就是所求作的互相垂直的两条直线．根据小晶设计的尺规作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明．

    证明：∵OC＝　 　，CP＝　 　，OP＝OP

    ∴△OPC≌△OPD

    ∴∠AOP＝∠BOP．

    ∴OE是△COD的高线（　 　）（填推理的依据）

    即OE⊥CD．

    ∴CD与OP互相垂直

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

    （1）在图1中证明CE=CF；

    （2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

    （3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．

    （1）求抛物线的函数解析式，并写出顶点D的坐标；
    （2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值；
    （3）在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

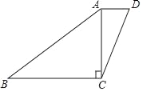
    【题目】如图，一张四边形纸片ABCD，AB＝20，BC＝16，CD＝13，AD＝5，对角线AC⊥BC．

    （1）求AC的长；

    （2）求四边形纸片ABCD的面积；

    （3）若将四边形纸片ABCD沿AC剪开，拼成一个与四边形纸片ABCD面积相等的三角形，直接写出拼得的三角形各边高的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点M在AC边上，点N从点C出发沿折线CB﹣BA运动到点A停止，点P是点C关于直线MN的对称点，连接MP，NP（当点N与点C，A重合时，点P均与点C重合）．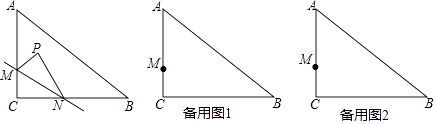

    （1）若CM=2，
    ①又当点N在CB上，MP∥BC时，则CN= ， MN=；
    （2）在（1）的条件下，求点P到AB边的距离的最小值，并求出当取得这个最小值时，点P运动路线的长是多少？（参考数据：sin54°=cos36°≈ ，sin36°=cos54°≈ ，结果保留π）
    （3）设MC=a（a＞2），其他条件不变，当有且只能有唯一的点P落在线段AB上时，直接写出a的取值范围 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有5张边长为2的正方形纸片，4张边长分别为2、3的矩形纸片，6张边长为3的正方形纸片，从其中取出若干张纸片，且每种纸片至少取一张，把取出的这些纸片拼成一个正方形（原纸张进行无空隙、无重叠拼接），则拼成正方形的边长最大为 （ ）

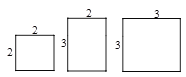
    A. 6B. 7C. 8D. 9

    查看答案和解析>>

    同步练习册答案