
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏY=ax2+bx“Μ3”κX÷αœύΫΜ”ΎA(“Μ1Θ§0)Θ§B(3Θ§0)Θ§PΈΣ≈ΉΈοœΏ…œΒΎΥΡœσœό…œΒΡΒψΘ°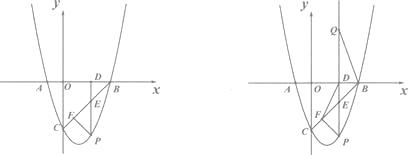
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΚ· ΐΙΊœΒ ΫΘ°
Θ®2Θ©ΙΐΒψPΉςPDΓΆX÷α”ΎΒψDΘ§PDΫΜBC”ΎΒψEΘ§Β±œΏΕΈPEΒΡ≥ΛΕ»Ήν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘ°
Θ®3Θ©Β±œΏΕΈPEΒΡ≥ΛΕ»Ήν¥σ ±Θ§ΉςPF ΓΆBC”ΎΒψFΘ§Ν§ΫαDFΘ°‘Ύ…δœΏPD…œ”–“ΜΒψQΘ§¬ζΉψΓœPQB=ΓœDFBΘ§Έ ‘ΎΉχ±ξ÷α…œ «Ζώ¥φ‘Ύ“ΜΒψRΘ§ ΙΒΟSΓςRBE=SΓςQBEΘΜ»γΙϊ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωRΒψΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©Ϋβ ΘΚΫΪA(“Μ1Θ§0)Θ§B(3Θ§0)Ζ÷±π¥ζ»κY=ax2+bx“Μ3ΒΟ ![]()
ΫβΒΟ ![]()
ΓύΗΟ≈ΉΈοœΏΒΡΚ· ΐΙΊœΒ ΫΈΣ y=x2-2x-3 ;
Θ®2Θ©Ϋβ ΘΚΑ―x=0¥ζ»κy=x2-2x-3 ;ΒΟΘ§y=-3 ,
ΓύC Θ®0Θ§-3Θ© Θ§
…η÷±œΏBCΒΡΫβΈω ΫΈΣy=kx+b,ΫΪC Θ®0Θ§-3Θ©”κB(3Θ§0)Θ§Ζ÷±π¥ζ»κΒΟ Θ§![]()
ΫβΒΟ ![]() ,
,
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣy=x-3 ;
…ηP Θ®m,m2-2m-3Θ©,
ΙΐΒψPΉςPDΓΆX÷α”ΎΒψDΘ§PDΫΜBC”ΎΒψE Θ§
E Θ®m,m-3Θ© ,
ΓύPE=(m-3)-(m2-2m-3)=-m2+3m=-(m-![]() )2+
)2+![]() ,
,
Ι Β±m=![]() ±Θ§PEΉν¥σΓΘ¥Υ ±P Θ®
±Θ§PEΉν¥σΓΘ¥Υ ±P Θ®![]() Θ§-
Θ§-![]() Θ©
Θ©
Θ®3Θ©Ϋβ ΘΚΒ±œΏΕΈPEΒΡ≥ΛΕ»Ήν¥σ ± ,P Θ®![]() Θ§-
Θ§-![]() Θ© Θ§E Θ®
Θ© Θ§E Θ®![]() Θ§-
Θ§-![]() Θ© Θ§PE =
Θ© Θ§PE =![]() ,
,
Γύ D(![]() ,0) ,
,0) ,
ΓύBD =![]()
ΓΏBΘ®3,0Θ© Θ§C Θ®0,3Θ©
ΓύOB=3=OC Θ§
ΓύOBCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ Θ§ΓύΓœOBC=45Γψ ,
‘ΎRtDBE÷–Θ§ΓœABC=45Γψ ,DB=![]() ,
,
ΓύBE=![]()
![]() ,ΓœDEB=45Γψ ,
,ΓœDEB=45Γψ ,
ΓύΓœPEF=45Γψ
‘ΎRtPEF÷– ΓœPEF=45Γψ PE=![]() ,
,
ΓύEF=![]() ,
,
ΓύBF=![]() ;
;
ΓΏΓœPQB=DFB ,ΓœDBE=ΓœDEB=45Γψ ,
ΓύQBEΓΉFDB ,
ΓύDBΓΟBEΘΫBFΓΟQE ,
Φ¥ ![]() ΓΟ
ΓΟ![]() =
=![]() ΓΟQE ,
ΓΟQE ,
ΓύQE=![]() ,
,
ΓΏSBQE=![]() ΓΛQEΓΛDB=
ΓΛQEΓΛDB=![]() =
=![]() ;
;
Β±RΒψ‘Ύx÷α…œ ±Θ§…ηR Θ®n,0Θ© ,BR=|3-n| ,
ΓύSRBE=![]() ,
,
Γύ![]() =
=![]() |3-n|ΓΛ
|3-n|ΓΛ![]()
|3-n|=![]()
n1=-![]() n2=
n2=![]() .
.
ΓύR (-![]() ,0) (
,0) (![]() ,0) ;
,0) ;
Β±R‘Ύy÷α…œΒΡ ±ΚρΘ§…ηRΘ®0Θ§zΘ©
SBER=SBRC-SREC
Γύ![]() =
=![]()
![]() 3ΓΝ|z-3|-
3ΓΝ|z-3|-![]() ΓΝ
ΓΝ![]() ΓΝ|z-3|
ΓΝ|z-3|
ΫβΒΟ z1=![]() ,z2=-
,z2=-![]() ;
;
ΓύR (0,-![]() ) (0,
) (0, ![]() ) ,
) ,
Ήέ…œΥυ ωΘ§RΒψΒΡΉχ±ξΈΣΘ®0 . ![]() Θ© Θ®0Θ§-
Θ© Θ®0Θ§- ![]() Θ©Θ®
Θ©Θ®![]() Θ§0Θ©Θ® -
Θ§0Θ©Θ® -![]() Θ§0Θ©
Θ§0Θ©
ΓΨΫβΈωΓΩΘ®1Θ©”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΫβΈω Ϋ ΘΜ
Θ®2Θ© Ήœ»«σ≥ωCΒψΒΡΉχ±ξΘ§‘Ό”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏBCΒΡΫβΈω ΫΈΣy=x-3 ΘΜ…ηP Θ®m,m2-2m-3Θ©Θ§ΙΐΒψPΉςPDΓΆX÷α”ΎΒψDΘ§PDΫΜBC”ΎΒψE Θ§¥”ΕχE Θ®m,m-3Θ© Θ§Ι PE=(m-3)-(m2-2m-3)=-m2+3m=-(m-![]() )2+
)2+![]() Θ§¥”Εχ«σ≥ωΒ±m=
Θ§¥”Εχ«σ≥ωΒ±m=![]() ±Θ§PEΉν¥σΘ§¥Υ ±P Θ®
±Θ§PEΉν¥σΘ§¥Υ ±P Θ®![]() Θ§-
Θ§-![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ© Ήœ»«σ≥ωE ΒψΉχ±ξΘ§PE≥ΛΕ»Θ§ΫχΕχΒΟ≥ωBDΒΡ≥ΛΕ»Θ§ΗυΨίB,CΝΫΒψΒΡΉχ±ξ≈–Εœ≥ωOBCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΫχΕχΗυΨίΙ¥Ι…Ε®άμΒΟ≥ωBEΒΡ≥ΛΘ§ΗυΨίΕ‘ΕΞΫ«œύΒ»ΒΟ≥ω‘ΎRtPEF÷–ΓœPEF=45ΓψΘ§ΗυΨίΙ¥Ι…Ε®άμΒΟ≥ωEFΒΡ≥ΛΘ§¥”ΕχΒΟ≥ωBFΒΡ≥ΛΘ§»ΜΚσ≈–Εœ≥ωQBEΓΉFDB ,ΗυΨίœύΥΤ»ΐΫ«–ΈΕ‘”Π±Ώ≥…±»άΐΝ–≥ωΖΫ≥ΧΘ§«σ≥ωQEΒΡ≥ΛΘ§ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ Ϋ«σ≥ωSBQEΘ§Β±RΒψ‘Ύx÷α…œ ±Θ§…ηR Θ®n,0Θ© ,BR=|3-n| ,ΗυΨίSΓςRBE=SΓςQBEΝ–≥ωΖΫ≥Χ«σ≥ωnΒΡ÷ΒΘ§ΒΟ≥ωRΒψΒΡΉχ±ξΘ§Β±R‘Ύy÷α…œΒΡ ±ΚρΘ§…ηRΘ®0Θ§zΘ© ”…SBER=SBRC-SRECΝ–≥ωΖΫ≥Χ«σ≥ωzΒΡ÷ΒΘ§‘Ό«σ≥ωRΒψ‘Ύy÷α…œΒΡ ±ΚρΒΡΉχ±ξΘ§¥”ΕχΒΟ≥ω±ΨΧβ¥πΑΗΓΘ



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»ΪΟφΕΰΚΔ’ΰ≤Ώ”Ύ2016Ρξ1‘¬1»’’ΐ Ϋ Β ©Θ§«≠Ρœ÷ίΡ≥÷–―ßΕ‘ΑΥΡξΦΕ≤ΩΖ÷―ß…ζΫχ––ΝΥΥφΜζΈ ΨμΒς≤ιΘ§Τδ÷–“ΜΗωΈ ΧβΓΑΡψΑ÷¬η»γΙϊΗχΡψΧμ“ΜΗωΒήΒήΘ®ΜρΟΟΟΟΘ©Θ§ΡψΒΡΧ§Ε» « ≤Ο¥ΘΩΓ±Ι≤”–»γœ¬ΥΡΗω―ΓœνΘ®“Σ«σΫω―Γ‘ώ“ΜΗω―ΓœνΘ©ΘΚ
AΘ°Ζ«≥Θ‘Η“β BΘ°‘Η“β CΘ°≤Μ‘Η“β DΘ°ΈόΥυΈΫ
»γΆΦ «ΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ§«κΫαΚœΆΦ÷––≈œΔΫβ¥π“‘œ¬Έ ΧβΘΚ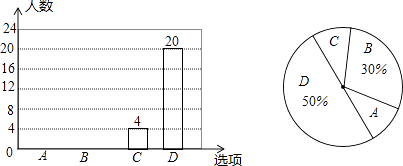
Θ®1Θ© ‘Έ ±Ψ¥ΈΈ ΨμΒς≤ι“ΜΙ≤Βς≤ιΝΥΕύ…ΌΟϊ―ß…ζΘΩ≤Δ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©»τΗΟΡξΦΕΙ≤”–450Οϊ―ß…ζΘ§«κΡψΙάΦΤ»ΪΡξΦΕΩ…Ρή”–Εύ…ΌΟϊ―ß…ζ÷ß≥÷Θ®Φ¥Χ§Ε»ΈΣΓΑΖ«≥Θ‘Η“βΓ±ΚΆΓΑ‘Η“βΓ±Θ©Α÷¬ηΗχΉ‘ΦΚΧμ“ΜΗωΒήΒήΘ®ΜρΟΟΟΟΘ©ΘΩ
Θ®3Θ©‘ΎΡξΦΕΜνΕ·ΩΈ…œΘ§άœ ΠΨωΕ®¥”±Ψ¥ΈΒς≤ιΜΊ¥πΓΑ≤Μ‘Η“βΓ±ΒΡΆ§―ß÷–ΥφΜζ―Γ»Γ2ΟϊΆ§―ßά¥ΧΗΧΗΥϊΟ«ΒΡœκΖ®Θ§Εχ±Ψ¥ΈΒς≤ιΜΊ¥πΓΑ≤Μ‘Η“βΓ±ΒΡ’β–©Ά§―ß÷–÷Μ”–“ΜΟϊΡ–Ά§―ßΘ§«κ”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®«σ―Γ»ΓΒΫΝΫΟϊΆ§―ß÷–Η’ΚΟ”–’βΈΜΡ–Ά§―ßΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ±Ώ≥ΛΈΣ3ΒΡ’ΐΖΫ–ΈABCD÷–Θ§ΒψEΓΔFΓΔGΓΔHΖ÷±π‘ΎABΓΔBCΓΔCDΓΔDA±Ώ…œΘ§«“¬ζΉψEB=FC=GD=HA=1Θ§BDΖ÷±π”κHGΓΔHFΓΔEFœύΫΜ”ΎMΓΔOΓΔN.Ηχ≥ω“‘œ¬Ϋα¬έΘ§
ΔΌHO=OF ΔΎ0F2=ONΓΛOBΔέHM=2MG ΔήSΓςHOM= ![]() Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ”–Θ® Θ©
Θ§Τδ÷–’ΐ»ΖΒΡΗω ΐ”–Θ® Θ©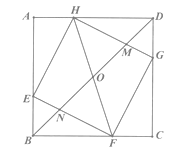
A.1
B.2
C.3
D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§œΏΕΈAB±μ Ψ“ΜΧθΕ‘’έΒΡ…ΰΉ”Θ§œ÷¥”PΒψΫΪ…ΰΉ”ΦτΕœΘ°ΦτΕœΚσΒΡΗςΕΈ…ΰΉ”÷–Ήν≥ΛΒΡ“ΜΕΈΈΣ30cmΘ°»τAP=![]() BPΘ§³t‘≠ά¥…ΰ≥ΛΈΣΘ®ΓΓΓΓΘ©cmΘ°
BPΘ§³t‘≠ά¥…ΰ≥ΛΈΣΘ®ΓΓΓΓΘ©cmΘ°
![]()
A. 55cmB. 75cmC. 55Μρ75cmD. 50Μρ75cm
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœCΘΫ90ΓψΘ§ΫΪΓςACE―ΊΉ≈AE’έΒΰ“‘ΚσCΒψ’ΐΚΟ¬δ‘ΎAB±Ώ…œΒΡΒψD¥ΠΘ°
Θ®1Θ©Β±ΓœBΘΫ28Γψ ±Θ§«σΓœAECΒΡΕ» ΐΘΜ
Θ®2Θ©Β±ACΘΫ6Θ§ABΘΫ10 ±Θ§
ΔΌ«σœΏΕΈBCΒΡ≥ΛΘΜ
ΔΎ«σœΏΕΈDEΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Χζ¬Ζ…œAΓΔBΝΫΒψœύΨύ25kmΘ§CΓΔDΈΣΝΫ¥εΉ·Θ§DAΓΆAB”ΎAΘ§CBΓΆAB”ΎBΘ§“―÷ΣDAΘΫ15kmΘ§CBΘΫ10kmΘ§œ÷‘Ύ“Σ‘ΎΧζ¬ΖAB…œΫ®“ΜΗωΆΝΧΊ≤ζΤΖ ’ΙΚ’ΨEΘ§ ΙΒΟCΓΔDΝΫ¥εΒΫE’ΨΒΡΨύάκœύΒ»Θ§‘ρE’Ψ”ΠΫ®‘ΎΨύA’ΨΕύ…Ό«ßΟΉ¥ΠΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ®“ε–¬‘ΥΥψΘΚΕ‘”Ύ»Έ“β Β ΐaΘ§bΘ®Τδ÷–aΓΌ0Θ©Θ§ΕΦ”–ab= ![]() ©¹
©¹ ![]() Θ§Β» Ϋ”“±Ώ «Ά®≥ΘΒΡΦ”Ζ®ΓΔΦθΖ®ΦΑ≥ΐΖ®‘ΥΥψΘ§άΐ»γ23=
Θ§Β» Ϋ”“±Ώ «Ά®≥ΘΒΡΦ”Ζ®ΓΔΦθΖ®ΦΑ≥ΐΖ®‘ΥΥψΘ§άΐ»γ23= ![]() ©¹
©¹ ![]() =
= ![]() +
+ ![]() =1Θ°
=1Θ°
Θ®1Θ©«σΘ®©¹2Θ©3ΒΡ÷ΒΘΜ
Θ®2Θ©»τx2=1Θ§«σxΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣADΓΆEFΘ§CEΓΆEFΘ§Γœ2+Γœ3=180ΓψΘ°
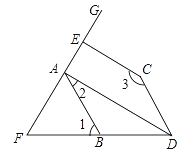
Θ®1Θ©«κΥΒΟςΓœ1=ΓœBDCΘΜ
Θ®2Θ©»τΓœ1=70ΓψΘ§DAΤΫΖ÷ΓœBDCΘ§ ‘«σΓœFABΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫ»Υ‘Ύ÷±œΏ≈ήΒά…œΆ§ΤπΒψΓΔΆ§÷’ΒψΓΔΆ§ΖΫœρ‘»ΥΌ≈ή≤Ϋ500ΟΉΘ§œ»ΒΫ÷’ΒψΒΡ»Υ‘≠ΒΊ–ίœΔΘ°“―÷ΣΦΉœ»≥ωΖΔ2ΟκΘ°‘Ύ≈ή≤ΫΙΐ≥Χ÷–Θ§ΦΉΓΔ““ΝΫ»ΥΒΡΨύάκyΘ®ΟΉΘ©”κ““≥ωΖΔΒΡ ±ΦδtΘ®ΟκΘ©÷°ΦδΒΡΙΊœΒ»γΆΦΥυ ΨΘ§Ηχ≥ω“‘œ¬Ϋα¬έΘΚΔΌa=8ΘΜΔΎb=92ΘΜΔέc=123Θ°Τδ÷–’ΐ»ΖΒΡ «Θ® Θ©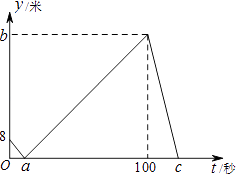
A.ΔΌΔΎΔέ
B.Ϋω”–ΔΌΔΎ
C.Ϋω”–ΔΌΔέ
D.Ϋω”–ΔΎΔέ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com