
【题目】如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
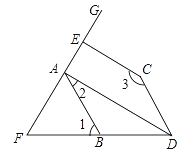
(1)请说明∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
【答案】(1)见解析;(2)55°.
【解析】
(1)先根据垂直的定义得出∠GAD=∠GEC=90°,故可得出AD∥CE,再由平行线的性质∠ADC+∠3=180°,据此可得出AB∥CD,进而可得出结论;
(2)先根据平行线的性质得出∠BDC=∠1=70°,再由DA平分∠BDC得出∠ADC的度数,进而得出∠2的度数,由∠FAB=∠FAD-∠2即可得出结论.
(1)∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°,
∴AD∥CE,
∴∠ADC+∠3=180°,
又∵∠2+∠3=180°,
∴∠2=∠ADC,
∴AB∥CD,
∴∠1=∠BDC;
(2) ∵AD⊥EF,
∴∠FAD=90°,
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC=![]() ∠BDC=
∠BDC=![]() ×70°=35°,
×70°=35°,
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD-∠2=90°-35°=55°.


科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90。 , 0B=2OA,点A在反比例函数 ![]() 的图象上,点B在反比例函数
的图象上,点B在反比例函数 ![]() 的图象上,则k的值是( )
的图象上,则k的值是( )
A.-4
B.4
C.-2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.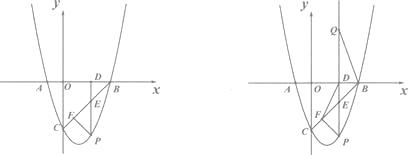
(1)求该抛物线的函数关系式.
(2)过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
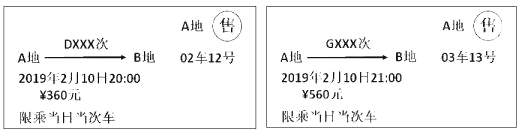
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1)现随机转动转盘一次,停止后,指针指向2的概率为;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
游戏规则:随机转动转盘两次,停止后,指针各指向一个数字,若两数之积为偶数,则小明胜;否则小华胜.
查看答案和解析>>
科目:初中数学 来源: 题型:
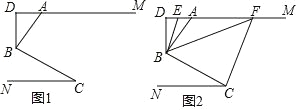
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小晶设计的“作互相垂直的两条直线”的尺规作图过程.
作法:如图,
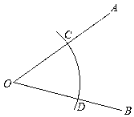
①在平面内任选一点O,作射线OA,OB;
②以O为圆心,以任意长为半径作弧,分别交OA于点C,交OB于点D;
③分别以C,D为圆心,以大于![]() CD的同样长为半径作弧,两弧交于∠AOB内部一点P;
CD的同样长为半径作弧,两弧交于∠AOB内部一点P;
④连接CP、PD;
⑤作直线OP,作直线CD,两直线相交于点E;则直线CD与OP就是所求作的互相垂直的两条直线.根据小晶设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OC= ,CP= ,OP=OP
∴△OPC≌△OPD
∴∠AOP=∠BOP.
∴OE是△COD的高线( )(填推理的依据)
即OE⊥CD.
∴CD与OP互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点M在AC边上,点N从点C出发沿折线CB﹣BA运动到点A停止,点P是点C关于直线MN的对称点,连接MP,NP(当点N与点C,A重合时,点P均与点C重合).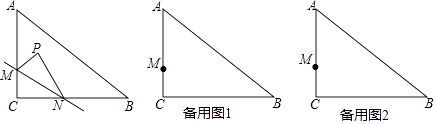
(1)若CM=2,
①又当点N在CB上,MP∥BC时,则CN= , MN=;
(2)在(1)的条件下,求点P到AB边的距离的最小值,并求出当取得这个最小值时,点P运动路线的长是多少?(参考数据:sin54°=cos36°≈ ![]() ,sin36°=cos54°≈
,sin36°=cos54°≈ ![]() ,结果保留π)
,结果保留π)
(3)设MC=a(a>2),其他条件不变,当有且只能有唯一的点P落在线段AB上时,直接写出a的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com