
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,
①HO=OF ②0F2=ON·OB③HM=2MG ④S△HOM= ![]() ,其中正确的个数有( )
,其中正确的个数有( )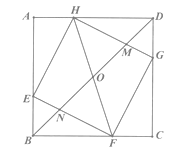
A.1
B.2
C.3
D.4
【答案】D
【解析】解 :∵四边形ABCD是正方形,
∴ AD=BC =AB=CD=3 , ,∠A=∠ABC=∠C=∠ADC=90° ,∠ADB=∠DBC=45° ,
∵EB=FC=GD=HA=1 ,
∴AE==CG=BF=DH=2 ,
∴AEH≌BFE≌CGF≌DHG ,
∴EH=EF=FG=GH ,∠AHE=∠BEF ,
∵∠AEH+∠AHE=90° ,
∴∠AEH+∠BEF=90° ,
∴∠HEF=90°
∴四边形EFGH是正方形 ,
∴∠OFN=45°
∴,∠OFN=∠OBF=45° ,
又∵∠FON=∠BOF ,
∴ONF∽OFB ,
∴ON∶OF=OF∶OB ,
∴0F2=ON·OB ; 故②正确;
在HOD与FOB中 ,
∵,∠ADB=∠DBC ,∠HOD=∠FOB ,HD=BF ,
∴HOD≌FOB ,
∴HO=OF ;故①正确;
∵SHDM∶SDMG=2∶1 ,SHDM∶SDMG=HM∶MG ,
∴HM∶MG =2∶1 ,
∴HM=2MG ;故③正确;
在RtAEH中,∠A=90° ,AH=1 ,AE=2 ,
根据勾股定理EH=![]() ,
,
∵S正方形EFGH=5 ,SHOG=S正方形EFGH=![]() ,
,
又∵SHOM∶SOMG=HM∶MG=2∶1 ,
∴S△HOM=![]() 。故④正确。
。故④正确。
故答案为 :D .
根据正方形的性质得出AD=BC =AB=CD=3 , ,∠A=∠ABC=∠C=∠ADC=90° ,∠ADB=∠DBC=45°,进而得出AE==CG=BF=DH=2 ,从而判断出AEH≌BFE≌CGF≌DHG ,根据全等三角形的性质得出EH=EF=FG=GH ,∠AHE=∠BEF ,根据三角形的内角和及同角的余角相等,平角的定义得出∠HEF=90° ,进而判断出四边形EFGH是正方形 ,根据正方形的性质判断出∠OFN=∠OBF=45° ,进而判断出ONF∽OFB ,根据相似三角形的性质得出0F2=ON·OB ;
根据AAS判断出HOD≌FOB ,根据全等三角形的性质得出HO=OF ;
根据角平分线的性质定理得出HDM与DMG如果分别以DH,DG为底的话,它们的高相等,从而得出SHDM∶SDMG=2∶1 又SHDM∶SDMG=HM∶MG ,HM∶MG =2∶1 ,HM=2MG ;
首先利用勾股定理得出EH的长,进而得出正方形EFGH的面积,根据正方形的性质得出SHOG=S正方形EFGH=![]() ,又SHOM∶SOMG=HM∶MG=2∶1 从而得出答案。
,又SHOM∶SOMG=HM∶MG=2∶1 从而得出答案。


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )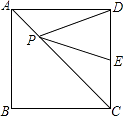
A.3 ![]()
B.10 ![]()
C.9
D.9 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90。 , 0B=2OA,点A在反比例函数 ![]() 的图象上,点B在反比例函数
的图象上,点B在反比例函数 ![]() 的图象上,则k的值是( )
的图象上,则k的值是( )
A.-4
B.4
C.-2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上.若测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最长边的长是( )

A. 2cm B. 4cm C. 2![]() cm D. 4
cm D. 4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC(AC+EC)为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线Y=ax2+bx一3与X轴相交于A(一1,0),B(3,0),P为抛物线上第四象限上的点.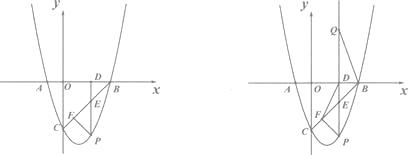
(1)求该抛物线的函数关系式.
(2)过点P作PD⊥X轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)当线段PE的长度最大时,作PF ⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE;如果存在,直接写出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
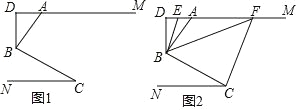
【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com