
【题目】如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC(AC+EC)为定值.
【答案】
(1)解:由B(3,m)可知OC=3,BC=m,又△ABC为等腰直角三角形,
∴AC=BC=m,OA=m﹣3,
∴点A的坐标是(3﹣m,0)
(2)解:∵∠ODA=∠OAD=45°
∴OD=OA=m﹣3,
则点D的坐标是(0,m﹣3).
又抛物线顶点为P(1,0),且过点B、D,
所以可设抛物线的解析式为:y=a(x﹣1)2,
得: ![]()
解得 ![]()
∴抛物线的解析式为y=x2﹣2x+1
(3)解:方法一:
证明:过点Q作QM⊥AC于点M,过点Q作QN⊥BC于点N,
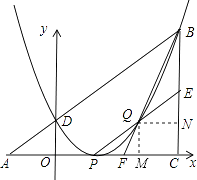
设点Q的坐标是(x,x2﹣2x+1),
则QM=CN=(x﹣1)2,MC=QN=3﹣x.
∵QM∥CE
∴△PQM∽△PEC
∴ ![]()
即 ![]() ,得EC=2(x﹣1)
,得EC=2(x﹣1)
∵QN∥FC
∴△BQN∽△BFC
∴ ![]()
即 ![]() ,得
,得 ![]()
又∵AC=4
∴FC(AC+EC)= ![]() [4+2(x﹣1)]=
[4+2(x﹣1)]= ![]() (2x+2)=
(2x+2)= ![]() ×2×(x+1)=8
×2×(x+1)=8
即FC(AC+EC)为定值8.
方法二:
设Q(t,t2﹣2t+1),B(3,4),
设直线BQ:y=kx+b,
∴lBQ:y=(t+1)x+1﹣3t,
把y=0代入y=(t+1)x+1﹣3t,
∴x= ![]() ,即F(
,即F( ![]() ,0),
,0),
∵P(1,0),Q(t,t2﹣2t+1),
∴lPQ:y=(t﹣1)x+1﹣t,
把x=3代入,∴y=2t﹣2,即E(3,2t﹣2),
∴FC(AC+EC)=(CX﹣FX)(CX﹣AX+EY﹣CY)=(3﹣ ![]() )(4+2t﹣2)=8.
)(4+2t﹣2)=8.
【解析】(1)求A点坐标可先求OA,利用线段之差即可求出;(2)先把抛物线解析式设成顶点式,再把B(3,m)、D点坐标(0,m-3)代入即可;(3) 线段的积可利用相似的性质对应边成比例,转化为其他线段的积.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板按如图放置,则下列结论:
①如果∠2=30°,则有AC∥DE;
②∠BAE+∠CAD =180°;
③如果BC∥AD,则有∠2=45°;
④如果∠CAD=150°,必有∠4=∠C;
正确的有( )
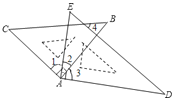
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要测量河岸相对的两点A、B之间的距离,先从B处出发与AB成![]() 方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转
方向,向前走50米到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转![]() 沿DE方向再走17米,到达E处,此时A、C、E三点在同一直线上,那么A、B两点间的距离为
沿DE方向再走17米,到达E处,此时A、C、E三点在同一直线上,那么A、B两点间的距离为![]()
![]()
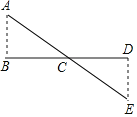
A. 10米 B. 12米 C. 15米 D. 17米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,
①HO=OF ②0F2=ON·OB③HM=2MG ④S△HOM= ![]() ,其中正确的个数有( )
,其中正确的个数有( )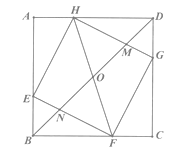
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:取三张大小、质地都相同的卡片,上面分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)如果和为奇数,则小明胜;若和为偶数,则小亮胜.你认为这个游戏规则对双方公平吗?做出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB表示一条对折的绳子,现从P点将绳子剪断.剪断后的各段绳子中最长的一段为30cm.若AP=![]() BP,則原来绳长为( )cm.
BP,則原来绳长为( )cm.
![]()
A. 55cmB. 75cmC. 55或75cmD. 50或75cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期三个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)本次调查中,张老师一共调查了 名同学,其中C类女生有 名,D类男生有 名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com