
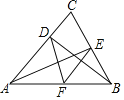
【题目】如图,在![]() 中,
中,![]() 于点E,
于点E,![]() 于点D;点F是AB的中点,连结DF,EF,设
于点D;点F是AB的中点,连结DF,EF,设![]() ,
,![]() ,则
,则![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由直角三角形斜边的中线等于斜边的一半可的AF=DF,BF=EF,从而由等腰三角形的性质得∠ADF=∠DAF,∠EBF=∠BEF,然后根据三角形外角的性质和三角形外角的性质可求得结论.
∵![]() 于点E,
于点E,![]() 于点D;点F是AB的中点,
于点D;点F是AB的中点,
∴AF=DF,BF=EF,
∴∠ADF=∠DAF,∠EBF=∠BEF,
∵∠AFD+∠DFE=∠EBF+∠BEF=2∠EBF,∠BFE+∠DFE=∠DAF+∠ADF=2∠DAF,
∠AFD+∠DFE+∠BFE+∠DFE
=2∠EBF+2∠DAF
=2(∠EBF+∠DAF)
= 2(180°-∠C)
=360°-2∠C,
∴180°+∠DFE=360°-2∠C,
∴180°+x=360°-2y,
∴![]() .
.
故选B.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题: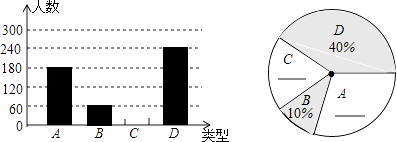
(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )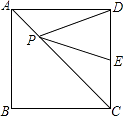
A.3 ![]()
B.10 ![]()
C.9
D.9 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=BC,D为AC中点,过点D作DE∥BC,交AB于点E.
(1)求证:AE=DE;
(2)若∠C=65°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线分别交AB、CD、BD于E、F、O,连接DE、BF.
(1)求证:四边形BEDF是菱形;
(2)若AB=8cm,BC=4cm,求四边形DEBF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A,C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的抛物线过点B,D.
(1)求点A的坐标(用m表示);
(2)求抛物线的解析式;
(3)设点Q为抛物线上点P至点B之间的一动点,连接PQ并延长交BC于点E,连接BQ并延长交AC于点F,试证明:FC(AC+EC)为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com