
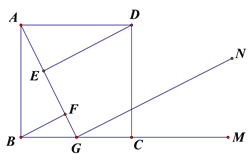
【题目】如图,正方形ABCD中,G是BC中点,DE⊥AG于E,BF⊥AG于F,GN∥DE,M是BC延长线上一点。
(1)求证:△ABF≌△DAE
(2)尺规作图:作∠DCM的平分线,交GN于点H(保留作图痕迹,不写作法和证明),试证明GH=AG。
【答案】(1)证明见解析;
(2)作图见解析,证明见解析.
【解析】解:∵ 四边形ABCD是正方形
∴ AB=BC=CD=DA
∠DAB=∠ABC=90°
 ∴ ∠DAE+∠GAB=90°
∴ ∠DAE+∠GAB=90°
∵ DE⊥AG BF⊥AG
∴ ∠AED=∠BFA=90°
∠DAE +∠ADE=90°
∴ ∠GAB =∠ADE
在△ABF和△DAE中
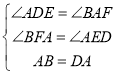
∴ △ABF≌△DAE
(2)作图略
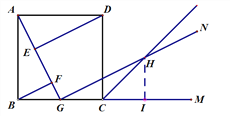 方法1:作HI⊥BM于点I
方法1:作HI⊥BM于点I
∵ GN∥DE
∴ ∠AGH=∠AED=90°
∴ ∠AGB+∠HGI=90°
∵ HI⊥BM
∴ ∠GHI+∠HGI=90°
∴ ∠AGB =∠GHI
∵ G是BC中点
∴ tan∠AGB=![]()
∴ tan∠GHI= tan∠AGB=![]()
∴ GI=2HI
∵ CH平分∠DCM
∴ ∠HCI=![]()
∴ CI=HI
∴ CI=CG=BG=HI
在△ABG和△GIH中
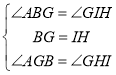
∴ △ABG≌△GIH
∴ AG=GH


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则![]() =___________.
=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥轴于B且S△ABO =
在第二象限的交点,AB⊥轴于B且S△ABO =![]() .
.
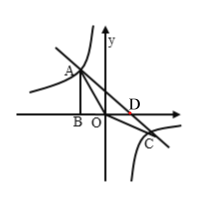
(1)求这两个函数的解析式.
(2)求直线与双曲线的两个交点A,C和直线AC与x轴的交点D的坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山坡上有一棵树AB,树底部B点到山脚C点的距离BC为![]() 米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
米,山坡的坡角为30°.小宁在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)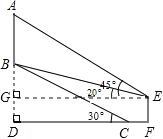
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.

求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
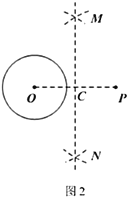
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)若P、Q分别从A、B同时出发,那么几秒后△PBQ的面积等于4cm2?
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5cm?
(3)在(1)中,△PBQ的面积能否等于7cm2? 请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
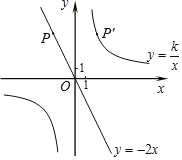
【题目】如图,已知直线y1=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y2=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求点P的坐标;
(2)求反比例函数的解析式,并直接写出当y2<2时自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com