
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,
;②存在,![]() 或
或![]() .
.
【解析】
(1)将点A、B坐标代入二次函数表达式,即可求解;
(2)①![]() ,即可求解;②分点P在直线BC下方、上方两种情况,分别求解即可.
,即可求解;②分点P在直线BC下方、上方两种情况,分别求解即可.
解:(1)将点A、B坐标代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线的表达式为:![]() …①,
…①,
令![]() ,则
,则![]() 或
或![]() ,
,
即点![]() ;
;
(2)①如图1,过点P作y轴的平行线交BC于点G,
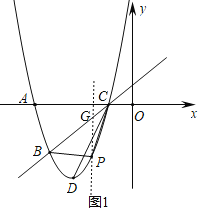
将点B、C的坐标代入一次函数表达式并解得:
直线BC的表达式为:![]() …②,
…②,
设点![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,![]() 有最大值,当
有最大值,当![]() 时,其最大值为
时,其最大值为![]() ;
;
②设直线BP与CD交于点H,
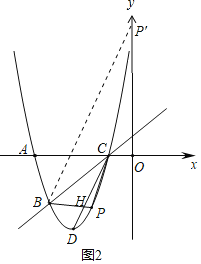
当点P在直线BC下方时,
![]() ,
,![]() 点H在BC的中垂线上,
点H在BC的中垂线上,
线段BC的中点坐标为![]() ,
,
过该点与BC垂直的直线的k值为﹣1,
设BC中垂线的表达式为:![]() ,将点
,将点![]() 代入上式并解得:
代入上式并解得:
直线BC中垂线的表达式为:![]() …③,
…③,
同理直线CD的表达式为:![]() …④,
…④,
联立③④并解得:![]() ,即点
,即点![]() ,
,
同理可得直线BH的表达式为:![]() …⑤,
…⑤,
联立①⑤并解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ;
;
当点![]() 在直线BC上方时,
在直线BC上方时,
![]() ,
,![]() ,
,
则直线BP′的表达式为:![]() ,将点B坐标代入上式并解得:
,将点B坐标代入上式并解得:![]() ,
,
即直线BP′的表达式为:![]() …⑥,
…⑥,
联立①⑥并解得:![]() 或
或![]() (舍去
(舍去![]() ),
),
故点![]() ;
;
故点P的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)解下列方程.
①![]() 根为______;
根为______;
②![]() 根为______;
根为______;
③![]() 根为______;
根为______;
(2)根据这类方程特征,写出第n个方程和它的根;
(3)请利用(2)的结论,求关于x的方程![]() (n为正整数)的根.
(n为正整数)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 中函数y与自变量x之间部分对应值如下表所示,点
中函数y与自变量x之间部分对应值如下表所示,点![]()
![]() 在函数图象上
在函数图象上
x | … | 0 | 1 | 2 | 3 | … |
y | … | m | n | 3 | n | … |
则表格中的m=______;当![]() 时,
时,![]() 和
和![]() 的大小关系为______.
的大小关系为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点B坐标为(0,m)(m>0),点A在x轴正半轴上,直线AB经过点A,B,且tan∠BAO=2.
(1)若点A的坐标为(3,0),求直线AB的表达式;
(2)反比例函数y=![]() 的图象与直线AB交于第一象限的C、D两点(BD<BC),当AD=2DB时,求k1的值(用含m的式子表示);
的图象与直线AB交于第一象限的C、D两点(BD<BC),当AD=2DB时,求k1的值(用含m的式子表示);
(3)在(1)的条件下,设线段AB的中点为E,过点E作x轴的垂线,垂足为M,交反比例函数y=![]() 的图象于点F.分别连接OE、OF,当△OEF与△OBE相似时,请直接写出满足条件的k2值.
的图象于点F.分别连接OE、OF,当△OEF与△OBE相似时,请直接写出满足条件的k2值.
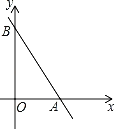
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司选派两人参加年度培训,小颖妈妈、张阿姨、李阿姨和王阿姨都报了名,若从4人中随机选派2人
(1)“小颖被选派”是 事件,“小颖妈妈被选派”是 事件.(填“不可能”或“必然“或“随机”)
(2)试用画树状图或列表的方法表示这次选派所有可能的结果,并求出“小颖妈妈被选派”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠B=∠DCA,AD∥BC,连结OD,AC,且OD与AC相交于点E.
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为4,且![]() =
=![]() ,求tan∠DCA的值.
,求tan∠DCA的值.
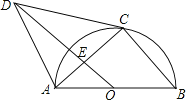
查看答案和解析>>
科目:初中数学 来源: 题型:
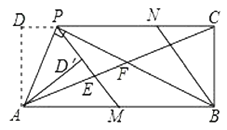
【题目】在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .连接
.连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .现有以下结论:①连接
.现有以下结论:①连接![]() ,则
,则![]() 垂直平分
垂直平分![]() ;②四边形
;②四边形![]() 是菱形;③
是菱形;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的结论是________(填写所有正确结论的序号).
.其中正确的结论是________(填写所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com