
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���B����Ϊ��0��m����m��0������A��x���������ϣ�ֱ��AB������A��B����tan��BAO��2��
��1������A������Ϊ��3��0������ֱ��AB�ı���ʽ��
��2������������y��![]() ��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��3���ڣ�1���������£����߶�AB���е�ΪE������E��x��Ĵ��ߣ�����ΪM��������������y��![]() ��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
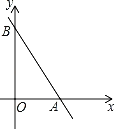
���𰸡���1��y����2x+6 ��2��4��3��![]() ��
��![]()
��������
��1����ͨ����ֱ�����������A�����꣬Ȼ����ݴ���ϵ�����������ֱ��AB�Ľ���ʽ��
��2����DE��OA����������ó�![]() �����DE����D�ĺ����꣬����AB�Ľ���ʽ��������꣬Ȼ����ݷ���������ͼ���ϵ�����������������k1��
�����DE����D�ĺ����꣬����AB�Ľ���ʽ��������꣬Ȼ����ݷ���������ͼ���ϵ�����������������k1��
��3�����ݹ��ɶ������AB��OE����һ�����BE��Ȼ��������������ε��������EF�ij����Ӷ����FM�ij����ó�F�����꣬Ȼ����ݷ���������ͼ���ϵ�����������������k2��
�⣺��1����A��3��0����B��0��m����m��0����
��OA��3��OB��m��
��tan��BAO��![]() ��2��
��2��
��m��6��
��ֱ��AB�Ľ���ʽΪy��kx+b��
����A��3��0����B��0��6���ã�![]() ��
��
��ã�b��6��k����2��
��ֱ��AB�Ľ���ʽΪy����2x+6��
��2����ͼ1��
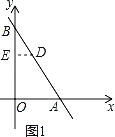
��AD��2DB��
��![]() ��
��
��DE��OA��
��![]() ��
��
��DE��![]() OA��1��
OA��1��
��D�ĺ�����Ϊ1��
����y����2x+6�ã�y��4��
��D��1��4����
��k1��1��4��4��
��3����ͼ2��
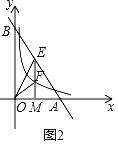
��A��3��0����B��0��6����
��E��![]() ��3����AB��
��3����AB��![]() ��
��
��OE��Rt��OABб���ϵ����ߣ�
��OE��![]() AB��
AB��![]() ��BE��
��BE��![]() ��
��
��EM��x�ᣬ
��F�ĺ�����Ϊ![]() ��
��
����OEF�ס�OBE��
��![]() ��
��![]() ��
��
��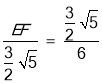 ��
��
��EF��![]() ��
��
��FM��3��![]() ��
��![]() ��
��
��F��![]() ��
��![]() ����
����
��k2��![]() ��
��![]() ��
��![]() ��
��
��ͼ3��
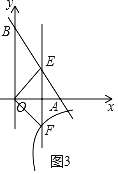
����OEF�ס�EOBʱ��
��![]() ��
��
��EF��OB��6��
��F��![]() ����3����
����3����
��k2����3��![]() ����
����![]() ��
��
��������������������k2ֵΪ![]() ��
��![]() ��
��


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�Ķ���A��C������ֱ��ǣ�0��3������4��0������ACB=90��AC=2BC������y=![]() ��k>0��x>0����ͼ����B����k��ֵΪ�� ��
��k>0��x>0����ͼ����B����k��ֵΪ�� ��
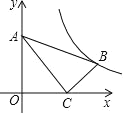
A.10B.11C.12D.13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ij����P��Χ10���ﷶΧ���а�����һ�Һ����ڵ�A���۲����P�ڱ�ƫ��60�����ú���������������8���ﵽ���B������ʱ�۲����Pǡ���ڱ�ƫ��45������������ּ��������������У����д�����Σ������˵�����ɣ����ο����ݣ�![]() ��1.73��
��1.73��
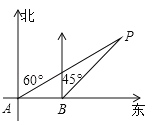
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ����
����![]() �ǶԽ���
�ǶԽ���![]() ��һ���㣬���߶�
��һ���㣬���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת120����
˳ʱ����ת120����![]() ������
������![]() ������
������![]() ���ӳ����ֱ�
���ӳ����ֱ�![]() �ڵ�
�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����֪![]() ����
����![]() ����СֵΪ
����СֵΪ![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ��ʮ���ˣ�ijУ������A������B�����C��������D�������������������Ϊ�˽�ѧ�����������������ϲ���������ȫУ��Χ�������ȡ������ѧ���������ʾ����飨ÿ���������ͬѧ����ѡ�����ֻ����4���������ѡ��һ�֣��������ݽ������������Ƴ���������ͳ��ͼ��δ����������
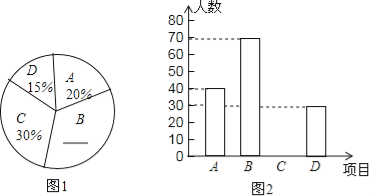
��1����ε����У�һ�������� ����ѧ����
��2���벹ȫ����ͳ��ͼ��
��3������3����ϲ������˶���ѧ����1����ϲ�������˶���ѧ���������μ�һ�����껥���������ѡ��2�˵����鳤�������������������˾�����ϲ������˶���ѧ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����
����![]() ��
��![]() ���㣬��x�����һ������ΪC������ΪD������CD��
���㣬��x�����һ������ΪC������ΪD������CD��
��1����������ߵı���ʽ��
��2����PΪ����������һ���㣨���B��C���غϣ������P�ĺ�����Ϊt��
�ٵ���P��ֱ��BC���·��˶�ʱ����![]() ����������ֵ��
����������ֵ��
�ڸ����������Ƿ���ڵ�P��ʹ��![]() �����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�����ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����
��1����b��1��a����![]() c����֤�����κ�����ͼ����x��һ����������ͬ�Ľ��㣻
c����֤�����κ�����ͼ����x��һ����������ͬ�Ľ��㣻
��2����a![]() 0��c��0���Ҷ��������ʵ��x������y
0��c��0���Ҷ��������ʵ��x������y![]() 1����4a+b2��ȡֵ��Χ��
1����4a+b2��ȡֵ��Χ��
��3��������ͼ�������㣨0��y1���ͣ�1��y2������y1y2��0����2a+3b+6c��0����ȷ�����κ���ͼ��Գ�����x�ύ��������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
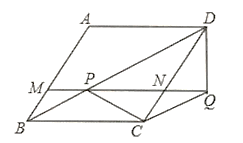
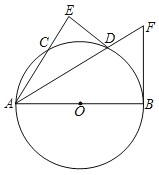
����Ŀ����ͼ��AB��ֱ����D��![]() ���е㣬DE��AC��AC���ӳ�����E����O������BF��AD���ӳ����ڵ�F��
���е㣬DE��AC��AC���ӳ�����E����O������BF��AD���ӳ����ڵ�F��
��1����֤��DE����O�����ߣ�
��2����̽��AE��AD��AB����֮��ĵ�����ϵ��
��3����DE=3����O�İ뾶Ϊ5����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����������ƶ�����ߣ�A��B���Ǿ�����C��D�������ͷ�����֧��ũ����������֪A��B���ǹ��з���500�֣�����A�Ƿ��ϱ�B����100�֣���A����C��D�����˷��ϵķ��÷ֱ�Ϊ20Ԫ/�ֺ�25Ԫ/�֣���B����C��D�����˷��ϵķ��÷ֱ�Ϊ15Ԫ/�ֺ�24Ԫ/�֣���C����Ҫ����240�֣�D����Ҫ����260�֣�
��1��A�Ǻ�B�Ǹ��ж��ٶַ��ϣ�
��2�����A������C�����x�֣����˷�ΪyԪ����y��x�ĺ�����ϵʽ��
��3���������˲���ʹ���˷����٣����������˷ѣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com