
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A.C的坐标分别是(0,3)、(4,0).∠ACB=90,AC=2BC,则函数y=![]() (k>0,x>0)的图象经过点B,则k的值为( )
(k>0,x>0)的图象经过点B,则k的值为( )
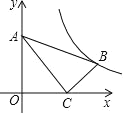
A.10B.11C.12D.13
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
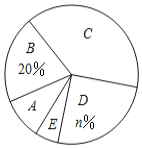
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】思维启迪:
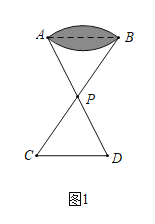
(1)如图1,![]() ,
,![]() 两点分别位于一个池塘的两端,小亮想用绳子测量
两点分别位于一个池塘的两端,小亮想用绳子测量![]() ,
,![]() 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达点
间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达点![]() 的点
的点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() (点
(点![]() 可以直接到达点
可以直接到达点![]() ),利用工具过点
),利用工具过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,此时测得
,此时测得![]() ,那么
,那么![]() ,
,![]() 间的距离是______
间的距离是______![]() .
.
思维探索:
(2)在![]() 和
和![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转,把点
顺时针旋转,把点![]() 在
在![]() 边上时
边上时![]() 的位置作为起始位置(此时点
的位置作为起始位置(此时点![]() 和点
和点![]() 位于
位于![]() 的两侧),设旋转角为
的两侧),设旋转角为![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
①如图2,当![]() 在起始位置时,猜想:
在起始位置时,猜想:![]() 与
与![]() 的数量关系和位置关系分别是_______;_______.
的数量关系和位置关系分别是_______;_______.
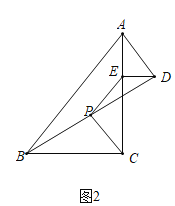
②如图3,当![]() ,点
,点![]() 落在
落在![]() 边上,请判断
边上,请判断![]() 与
与![]() 的数量关系和位置关系,并证明你的结论.
的数量关系和位置关系,并证明你的结论.
③当![]() 时,若
时,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,小聪同学利用直尺和圆规完成了如下操作:
中,小聪同学利用直尺和圆规完成了如下操作:
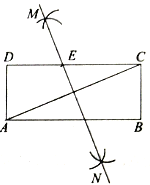
①分别以点![]() 和
和![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() 和
和![]() ;
;
②作直线![]() ,交
,交![]() 于点
于点![]() .
.
请你观察图形解答下列问题:
(1)![]() 与
与![]() 的位置关系:
的位置关系:
直线![]() 是线段
是线段![]() 的____________线;
的____________线;
(2)若![]() ,
,![]() ,求矩形的对角线
,求矩形的对角线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解下列方程.
①![]() 根为______;
根为______;
②![]() 根为______;
根为______;
③![]() 根为______;
根为______;
(2)根据这类方程特征,写出第n个方程和它的根;
(3)请利用(2)的结论,求关于x的方程![]() (n为正整数)的根.
(n为正整数)的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An.(n≥3,n是整数)处,那么线段AnA的长度为________(n≥3,n是整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
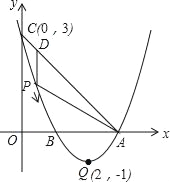
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点B坐标为(0,m)(m>0),点A在x轴正半轴上,直线AB经过点A,B,且tan∠BAO=2.
(1)若点A的坐标为(3,0),求直线AB的表达式;
(2)反比例函数y=![]() 的图象与直线AB交于第一象限的C、D两点(BD<BC),当AD=2DB时,求k1的值(用含m的式子表示);
的图象与直线AB交于第一象限的C、D两点(BD<BC),当AD=2DB时,求k1的值(用含m的式子表示);
(3)在(1)的条件下,设线段AB的中点为E,过点E作x轴的垂线,垂足为M,交反比例函数y=![]() 的图象于点F.分别连接OE、OF,当△OEF与△OBE相似时,请直接写出满足条件的k2值.
的图象于点F.分别连接OE、OF,当△OEF与△OBE相似时,请直接写出满足条件的k2值.
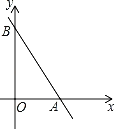
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com