
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
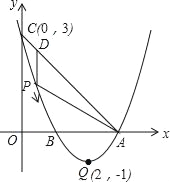
【答案】(1) y=x2﹣4x+3;(2) P1(1,0),P2(2,﹣1);(3) F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).
【解析】试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点式,然后将函数图象经过的C点坐标代入上式中,即可求出抛物线的解析式;
(2)由于PD∥y轴,所以∠ADP≠90°,若△ADP是直角三角形,可考虑两种情况:
①以点P为直角顶点,此时AP⊥DP,此时P点位于x轴上(即与B点重合),由此可求出P点的坐标;
②以点A为直角顶点,易知OA=OC,则∠OAC=45°,所以OA平分∠CAP,那么此时D、P关于x轴对称,可求出直线AC的解析式,然后设D、P的横坐标,根据抛物线和直线AC的解析式表示出D、P的纵坐标,由于两点关于x轴对称,则纵坐标互为相反数,可据此求出P点的坐标;
(3)很显然当P、B重合时,不能构成以A、P、E、F为顶点的四边形,因为点P、F都在抛物线上,且点P为抛物线的顶点,所以PF与x轴不平行,所以只有(2)②的一种情况符合题意,由②知此时P、Q重合;假设存在符合条件的平行四边形,那么根据平行四边形的性质知:P、F的纵坐标互为相反数,可据此求出F点的纵坐标,代入抛物线的解析式中即可求出F点的坐标.
试题解析:(1)∵抛物线的顶点为Q(2,﹣1),
∴设抛物线的解析式为y=a(x﹣2)2﹣1,
将C(0,3)代入上式,得:
3=a(0﹣2)2﹣1,a=1;
∴y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)分两种情况:
①当点P1为直角顶点时,点P1与点B重合;
令y=0,得x2﹣4x+3=0,解得x1=1,x2=3;
∵点A在点B的右边,
∴B(1,0),A(3,0);
∴P1(1,0);
②当点A为△AP2D2的直角顶点时;
∵OA=OC,∠AOC=90°,
∴∠OAD2=45°;
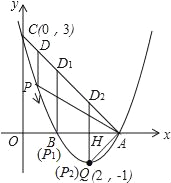
当∠D2AP2=90°时,∠OAP2=45°,
∴AO平分∠D2AP2;
又∵P2D2∥y轴,
∴P2D2⊥AO,
∴P2、D2关于x轴对称;
设直线AC的函数关系式为y=kx+b(k≠0).
将A(3,0),C(0,3)代入上式得:
![]() ,
,
解得![]() ;
;
∴y=﹣x+3;
设D2(x,﹣x+3),P2(x,x2﹣4x+3),
则有:(﹣x+3)+(x2﹣4x+3)=0,
即x2﹣5x+6=0;
解得x1=2,x2=3(舍去);
∴当x=2时,y=x2﹣4x+3=22﹣4×2+3=﹣1;
∴P2的坐标为P2(2,﹣1)(即为抛物线顶点).
∴P点坐标为P1(1,0),P2(2,﹣1);
(3)由(2)知,当P点的坐标为P1(1,0)时,不能构成平行四边形;
当点P的坐标为P2(2,﹣1)(即顶点Q)时,
平移直线AP交x轴于点E,交抛物线于F;
∵P(2,﹣1),
∴可设F(x,1);
∴x2﹣4x+3=1,
解得x1=2﹣![]() ,x2=2+
,x2=2+![]() ;
;
∴符合条件的F点有两个,
即F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形OA1A2的直角边OA1在y轴的正半轴上,且OA1=A1A2=1,以OA2为直角边作第二个等腰直角三角形OA2A3,以OA3为直角边作第三个等腰直角三角形OA3A4,…,依此规律,得到等腰直角三角形OA2017A2018,则点A2017的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
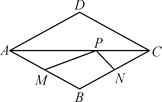
【题目】点P是菱形ABCD的对角线AC上的一个动点,已知AB=1,∠ADC=120°, 点M,N分别是AB,BC边上的中点,则△MPN的周长最小值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从C市运往B市的救灾物资为x吨.
(1)请填写下表;
A | B | 合计(吨) | |
C |
| x | 240 |
D |
|
| 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为W元,求W与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从C市到B市的路况得到了改善,缩短了运输时间,运费每吨减少n元(N>0),其余路线运费不变,若C、D两市的总运费的最小值不小于10080元,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某国际化学校实行小班制教学,七年级四个班共有学生(6m-3n)人,一班有学生m人,二班人数比一班人数的两倍少n人,三班人数比二班人数的一半多12人.
(1)求三班的学生人数(用含m.n的式子表示);
(2)求四班的学生人数;(用含m.n的式子表示);
(3)若四个班共有学生120人,求二班比三班多的学生人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
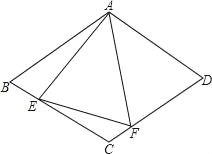
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线y=2x+m与y=![]() (n≠0)交于A,B两点,且点A的坐标为(1,4).
(n≠0)交于A,B两点,且点A的坐标为(1,4).
(1)求此直线和双曲线的表达式;
(2)过x轴上一点M作平行于y轴的直线1,分别与直线y=2x+m和双曲线y=![]() (n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.
(n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知点A(0,3)、点B(3,0),一次函数y=2x的图象与直线AB交于点M.
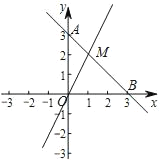
(1)求直线AB的函数解析式及M点的坐标;
(2)若点N是x轴上一点,且△MNB的面积为6,求点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com