
【题目】如图直线y=2x+m与y=![]() (n≠0)交于A,B两点,且点A的坐标为(1,4).
(n≠0)交于A,B两点,且点A的坐标为(1,4).
(1)求此直线和双曲线的表达式;
(2)过x轴上一点M作平行于y轴的直线1,分别与直线y=2x+m和双曲线y=![]() (n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.
(n≠0)交于点P,Q,如果PQ=2QM,求点M的坐标.

科目:初中数学 来源: 题型:
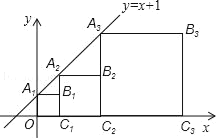
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2…、正方形AnBnnCn﹣1按如图方式放置,点A1、A2、A3、…在直线y=x+1上,点C1、C2、C3、…在x轴上.已知A1点的坐标是(0,1),则点B3的坐标为_____,点Bn的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
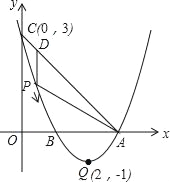
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
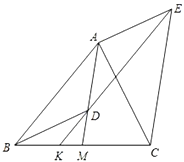
【题目】如图,![]() 是
是![]() 的中线,点
的中线,点![]() 是线段
是线段![]() 上一点(不与点
上一点(不与点![]() 重合).过点
重合).过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)判断线段![]() 、
、![]() 的关系,并说明理由.
的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,点A 的坐标为(1,0),P 是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).若点P到x轴的距离为![]() ,则m+n 的最小值为___.
,则m+n 的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予3a实际意义的例子中不正确的是![]()
![]()
A. 若葡萄的价格是3元![]() 千克,则3a表示买a千克葡萄的金额
千克,则3a表示买a千克葡萄的金额
B. 若a表示一个等边三角形的边长,则3a表示这个等边三角形的周长
C. 将一个小木块放在水平桌面上,若3表示小木块与桌面的接触面积,a表示桌面受到的压强,则3a表示小木块对桌面的压力
D. 若3和a分别表示一个两位数中的十位数字和个位数字,则3a表示这个两位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,D为⊙O上一点,AT 平分∠BAD交⊙O于点 T,过 T 作AD的垂线交 A D的延长线于点 C。
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,CT=![]() ,求AD的长。
,求AD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形![]() 是半高三角形,且斜边
是半高三角形,且斜边![]() ,则它的周长等于_________.
,则它的周长等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂一周计划生产700台相同型号的电子玩具,平均每天生产100台,由于各种原因实际每天生产量与计划量相比有出入(超过为正,不足为负,单位:台),下表是某周每天的生产情况
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
产量 | +5 | -3 | -4 | +10 | -6 | +12 | -7 |
(1)根据记录可知前三天共生产______台;
(2)产量最多的一天比产量最少的一天多生产______台;
(3)该厂实行计件工资制,每生产一台电子玩具40元,若按周计算,超额完成任务,超出部分每台50元;若未完成任务,生产出的电子玩具每台只能按35元发工资.那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com