
����Ŀ��Ϊӭ��ʮ���ˣ�ijУ������A������B�����C��������D�������������������Ϊ�˽�ѧ�����������������ϲ���������ȫУ��Χ�������ȡ������ѧ���������ʾ����飨ÿ���������ͬѧ����ѡ�����ֻ����4���������ѡ��һ�֣��������ݽ������������Ƴ���������ͳ��ͼ��δ����������
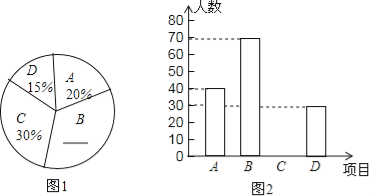
��1����ε����У�һ�������� ����ѧ����
��2���벹ȫ����ͳ��ͼ��
��3������3����ϲ������˶���ѧ����1����ϲ�������˶���ѧ���������μ�һ�����껥���������ѡ��2�˵����鳤�������������������˾�����ϲ������˶���ѧ���ĸ��ʣ�
���𰸡���1��200����2����ͼ����������3��![]() .
.
��������
��1������A�����������ռ�İٷֱȣ����������������
��2��������1��ȥA��C��D����ռ�İٷֱȣ��������B��ռ�İٷֱȣ���������������ռ�İٷֱȣ����C���������Ӷ���ȫͼ�Σ�
��3��������������оٷ����ٳ����еĿ��ܣ�ע��Ҫ�������ز�©���ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�
��1���������ѧ����![]() =200��������
=200��������
�ʴ�Ϊ200��
��2��B��ռ�İٷֱ���1-15%-20%-30%=35%��
C�������ǣ�200��30%=60��������
��ͼ���£�
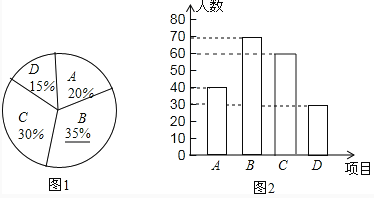
��3����A1��A2��A3��ʾ3��ϲ������˶���ѧ����B��ʾ1�������˶���ѧ����
���4����ѡ��2�˵�����У���A1��A2������A1��A3������A1��B������A2��A3������A2��B������A3��B��������6�֣�
ѡ����2�˶�����ϲ������˶���ѧ���У�A1��A2������A1��A3������A2��A3������3�֣�
�����˾�����ϲ������˶���ѧ���ĸ���![]() ��
��


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
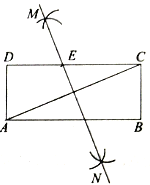
����Ŀ����ͼ���ھ���![]() �У�С��ͬѧ����ֱ�ߺ�Բ����������²�����
�У�С��ͬѧ����ֱ�ߺ�Բ����������²�����
�ٷֱ��Ե�![]() ��
��![]() ΪԲ�ģ��Դ���
ΪԲ�ģ��Դ���![]() �ij�Ϊ�뾶�����������ཻ�ڵ�
�ij�Ϊ�뾶�����������ཻ�ڵ�![]() ��
��![]() ��
��
����ֱ��![]() ����
����![]() �ڵ�
�ڵ�![]() .
.
����۲�ͼ�ν���������⣺
��1��![]() ��
��![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
ֱ��![]() ���߶�
���߶�![]() ��____________�ߣ�
��____________�ߣ�
��2����![]() ��
��![]() ������εĶԽ���
������εĶԽ���![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C�ǻ�AB���е㣬����AC���ӳ�����D��ʹCD��AC����E��OB��һ�㣬��![]() ��CE���ӳ��߽�D���ӳ����ڵ�F��AF����O�ڵ�H������BH��
��CE���ӳ��߽�D���ӳ����ڵ�F��AF����O�ڵ�H������BH��

��1����֤��BD����O�����ߣ�
��2����OB��2ʱ����AH�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��6��BC��3����E���߶�BA�ϴ�B����ÿ��1����λ���ٶȳ�����A���˶���F������CD��һ���㣬�ڵ�E��F�˶��Ĺ�����ʼ�ձ���EF��5����CF>BE����P��EF���е㣬����AP�����E�˶�ʱ��Ϊts��



��1���ڵ�E��F�˶��Ĺ�������AP�ij��ȴ���һ����Сֵ����AP�ij���ȡ����Сֵʱ����P��λ��Ӧ���� ��
��2����AP��EFʱ�������ʱt��ֵ
��3����PΪԲ������P������P�����ABCD��������ֱ�߶�����ʱ�������ʱt��ֵ����ָ����ʱ��P�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����¸ڹ����پ�ҵ��ij���������涨����ҵ���ɱ����ṩ��Ʒ���¸���Ա�������ۣ��ɱ����������֮��IJ���������е������������Ͷ�����۱���������һ�ֶ�ͯ��������֪���ֶ�ͯ�����ijɱ���Ϊÿ��12Ԫ��������Ϊÿ��16Ԫ��ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮��Ĺ�ϵ��������һ�κ�����
��Ԫ��֮��Ĺ�ϵ��������һ�κ�����![]() ��
��
��1�������ڿ�ʼ��ҵ�ĵ�1�콫���۵��۶�Ϊ17Ԫ����ô������һ��Ϊ���е����ܲ��Ϊ����Ԫ��
��2���������õ�����Ϊ![]() ��Ԫ���������۵���Ϊ����Ԫʱ��ÿ��ɻ���������
��Ԫ���������۵���Ϊ����Ԫʱ��ÿ��ɻ���������
��3����۲��Ź涨���������������۵��۲��ø���24Ԫ�����������Ҫÿ���õ�������216Ԫ����ô����ÿ��Ϊ���е����ܲ������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���B����Ϊ��0��m����m��0������A��x���������ϣ�ֱ��AB������A��B����tan��BAO��2��
��1������A������Ϊ��3��0������ֱ��AB�ı���ʽ��
��2������������y��![]() ��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��3���ڣ�1���������£����߶�AB���е�ΪE������E��x��Ĵ��ߣ�����ΪM��������������y��![]() ��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
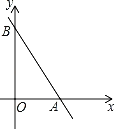
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
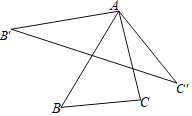
����Ŀ����ͼ����![]() �ı�
�ı�![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() �õ�
�õ�![]() ����AC���ŵ�A��ʱ����ת
����AC���ŵ�A��ʱ����ת![]() �õ�
�õ�![]() ������
������![]() ����
����![]() ʱ�����dz�
ʱ�����dz�![]() ��
��![]() �ġ�˫�������Ρ�������ȱ�
�ġ�˫�������Ρ�������ȱ�![]() �ı߳�Ϊa����ô���ġ�˫�������Ρ��������__________���ú�a�Ĵ���ʽ��ʾ����
�ı߳�Ϊa����ô���ġ�˫�������Ρ��������__________���ú�a�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y����x+4�ֱ���x�ᡢy�ύ�ڵ�A��B��˫����![]() ��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ츴��������ij��ҵ�����������ʣ��ݵ����֪��2���������3��С����һ�ο�������600�䣻5���������6��С����һ�ο�������1350�䣮
(1)��1���������1��С����һ�ο��Էֱ�������������ʣ�
(2)�ƻ������ֻ�����12�������������ʣ�ÿ�������һ�������5 000Ԫ��ÿ��С����һ�������3000Ԫ�����������ʲ�����1500�䣬���ܷ���С��54000Ԫ�������г��������䷽��,��ָ�����ַ�������������٣����ٷ����Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com