
【题目】如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.



(1)在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
(2)当AP⊥EF时,求出此时t的值
(3)以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
【答案】(1)AD的中点;(2)t=![]() (s);(3)
(s);(3)![]() ,
,![]() ;
;![]() ,
,![]()
【解析】
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,在运动过程中,根据垂线段最短可得P为AD的中点时,AP的长度最小;
(2)首先过点E作EG⊥CD于点G,易证得△APE∽△EGF,然后由相似三角形的对应边成比例,求得AE的长,继而求得答案;
(3)分两种情况考虑:当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,连接PQ,PR,PN,如图3所示,可得出四边形AQPR和四边形RPND为两个全等的正方形,其边长为大正方形边长的一半,在直角三角形PQE中,由PE与PQ的长,利用勾股定理求出EQ的长,进而由BA+AQ-EQ求出BE的长,即为t的值,并求出此时⊙P的半径;当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,如图4所示,同理求出BE的长,即为t的值,并求出此时⊙P的半径.
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,如图所示:根据垂线段最短可得P为AD的中点时,AP的长度最小;
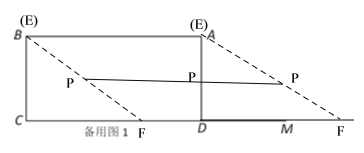
故答案为:AD的中点;
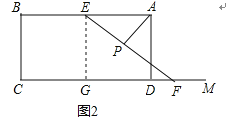
(2)过点E作EG⊥CD于点G,如图2
则四边形BCGE是矩形,
∴EG=BC=3,AB∥CD,
∴FG=![]() ,∠AEP=∠EFG
,∠AEP=∠EFG
∵AP⊥EF,
∴∠APE=∠EGF=90°,
∴△APE∽△EGF,
∴ ![]()
∴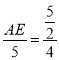
∴AE=![]()
∴BE=6-![]()
∴t=![]() (s)
(s)
(3)如图3,当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,
连接PQ、PR、PN,则PQ⊥AB、PR⊥AD、PN⊥CD,
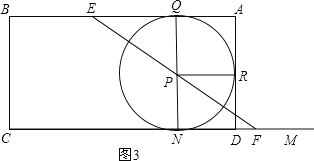
则四边形AQPR与四边形RPND为两个全等的正方形,
∴PQ=AQ=AR=DR=![]() AD=
AD=![]() ,
,
在Rt△PQE中,EP=![]() ,由勾股定理可得:EQ=2,
,由勾股定理可得:EQ=2,
∴BE=BA-EQ-AQ=6-2-![]() =
=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() ;
;
如图4,当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,
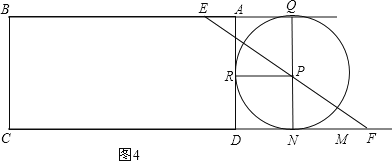
类比图3可得,EQ=2,AQ=![]() ,
,
∴BE=BA+AQ-EQ=6+![]() -2=
-2=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】小亮在课余时间写了三个算式:![]() ,
,![]() ,
,![]() ,通过认真观察,发现任意两个连续奇数的平方差是
,通过认真观察,发现任意两个连续奇数的平方差是![]() 的倍数.
的倍数.
验证
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设两个连续奇数为![]() ,
,![]() (其中
(其中![]() 为正整数),写出它们的平方差,并说明结果是
为正整数),写出它们的平方差,并说明结果是![]() 的倍数;
的倍数;
延伸
直接写出两个连续偶数的平方差是几的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
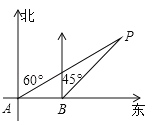
【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
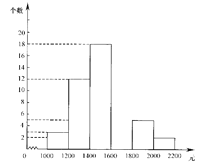
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
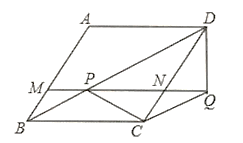
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转120°到
顺时针旋转120°到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)已知![]() ,若
,若![]() 的最小值为
的最小值为![]() ,求菱形
,求菱形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
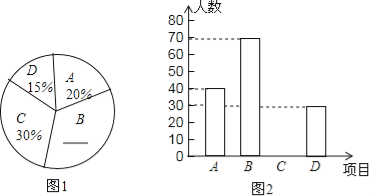
(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0).
(1)若b=1,a=﹣![]() c,求证:二次函数的图象与x轴一定有两个不同的交点;
c,求证:二次函数的图象与x轴一定有两个不同的交点;
(2)若a![]() 0,c=0,且对于任意的实数x,都有y
0,c=0,且对于任意的实数x,都有y![]() 1,求4a+b2的取值范围;
1,求4a+b2的取值范围;
(3)若函数图象上两点(0,y1)和(1,y2)满足y1y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),其对称轴为直线x=1,下列结论中正确的是( )
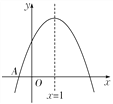
A. abc>0 B. 2a-b=0 C. 4a+2b+c<0 D. 9a+3b+c=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com