
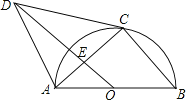
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠B=∠DCA,AD∥BC,连结OD,AC,且OD与AC相交于点E.
(1)求证:CD与⊙O相切;
(2)若⊙O的半径为4,且![]() =
=![]() ,求tan∠DCA的值.
,求tan∠DCA的值.
【答案】(1)见解析 (2)![]()
【解析】
(1)连接OC,易证∠DCA=∠OCB,由于∠ACO+∠OCB=90°,所以∠ACO+∠DCA=90°,即∠DCO=90°,从而可证CD与⊙O相切;
(2) 过点O作OF∥BC,交CD于点F,交AC于点G,由于△AED∽△GEO,再利用对应边成比例,设AD=5x,OG=2x,进一步证明△ADC∽△CAB,所以AC2=ADBC,所以AC=![]() ,最后根据锐角三角函数即可求出tan∠B的值.
,最后根据锐角三角函数即可求出tan∠B的值.
解:(1)连接OC,如下图所示:
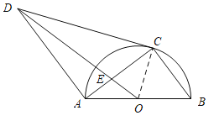
∵OC=OB,
∴∠OCB=∠B,
∵∠B=∠DCA,
∴∠DCA=∠OCB,
∵∠ACO+∠OCB=90°,
∴∠ACO+∠DCA=90°,
即∠DCO=90°,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)过点O作OF∥BC,交CD于点F,交AC于点G,
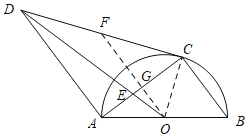
∵AD∥BC,
∴AD∥OG,
∴△AED∽△GEO,
![]() ,
,
设AD=5x,OG=2x,
∵∠ACB=90°,
∴由垂径定理可知:点G为AC的中点,
∴OG是△ACB的中位线,
∴BC=2OG=4x,
∵∠B=∠DCA,∠DAC=∠ACB=90°,
∴△ADC∽△CAB
∴![]() ,
,
∴AC2=AD×BC,
∴AC=![]() ,
,
∴tan∠B=![]() .
.
故答案为:tan∠B=![]() .
.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】为阻断新冠疫情向校园蔓延,确保师生生命安全和身体健康,教育部通知,2020年春季学期延期开学,利用网上平台,停课不停学”,某校对初三全体学生数学线上学习情况进行调查,随机抽取部分学生的4月月诊断性测试成绩,按由高到低分为A,B,C,D四个等级,根据调查的数据绘制成如下的条形统计图和扇形统计图,请根据图中的信息,解答下列问题:
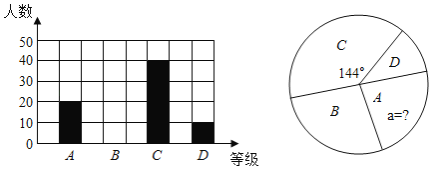
(1)该校共抽查了 名同学的数学测试成绩,扇形统计图中A等级所占的百分比a= ;
(2)补全条形统计图;
(3)若该校初三共有1180名同学,请估计该校初三学生数学测试成绩优秀(测试成绩B级以上为优秀,含B级)约有 名;
(4)该校老师想从两男、两女四位学生中随机选择两位了解平时线上学习情况,请用列表或画树形图的方法求出恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴的另一个交点为C,顶点为D,连结CD.
两点,与x轴的另一个交点为C,顶点为D,连结CD.
(1)求该抛物线的表达式;
(2)点P为该抛物线上一动点(与点B、C不重合),设点P的横坐标为t.
①当点P在直线BC的下方运动时,求![]() 的面积的最大值;
的面积的最大值;
②该抛物线上是否存在点P,使得![]() 若存在,求出所有点P的坐标;若不存在,请说明理由.
若存在,求出所有点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
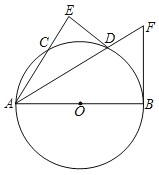
【题目】如图,AB是直经,D是![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.
(1)求证:DE是⊙O的切线.
(2)试探究AE,AD,AB三者之间的等量关系.
(3)若DE=3,⊙O的半径为5,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
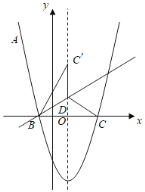
【题目】如图,抛物线y=![]() ﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
﹣2x﹣3经过点A(﹣2,a),与x轴相交于B、C两点(B点在C点左侧).
(1)求a的值及B、C两点坐标;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△B![]() D,若点
D,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点D的坐标;
和点D的坐标;
(3)设P(m,-3)是该抛物线上一点,点Q为抛物线的顶点,在x轴、y轴分别找点M、N,使四边形MNQP的周长最小,请求出点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
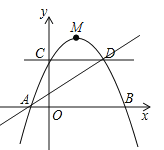
【题目】如图,已知顶点为![]() 的抛物线过点
的抛物线过点![]() ,交
,交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上一动点.
是抛物线上一动点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 上方时,求
上方时,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
![]() 过点
过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若将
,若将![]() 沿
沿![]() 翻折点
翻折点![]() 的对应点为点
的对应点为点![]() .是否存在点
.是否存在点![]() ,使
,使![]() 恰好落在
恰好落在![]() 轴上?若存在,求出点
轴上?若存在,求出点![]() 的坐标:若不存在,说明理由.
的坐标:若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC,求证:PD//AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB=![]() .
.
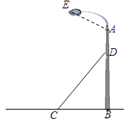
(1)求钢缆CD的长度。
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com