
【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
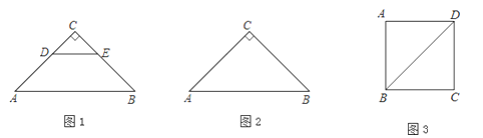
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为![]() , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
, 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
【答案】(1)①补图见解析;②证明见解析;③CM=![]() .(2)1.
.(2)1.
【解析】
(1)①根据旋转的特性画出图象;②由∠ACD、∠BCE均与∠DCB互余可得出∠ACD=∠BCE,由△ABC和△CDE都是等腰直角三角形可得出AC=BC、DC=EC,结合全等三角形的判定定理SAS即可得出△ADC≌△BEC,从而得出AD=BE,再由∠BCE=∠ADC=135°,∠CED=45°即可得出∠AEB=90°,即证出AD⊥BE;③依照题意画出图形,根据组合图形的面积为两个三角形的面积和可用AE,BE去表示CM;
(2)根据题意画出图形,比照(1)③的结论以及利用全等三角形的性质,套入数据即可得出结论.
(1)①依照题意补全图2,如下图(一)所示.

②证明:∵∠ACD+∠DCB=∠ACB=90°,∠BCE+∠DCB=∠DCE=90°,
∴∠ACD=∠BCE.
∵△ABC和△CDE都是等腰直角三角形,
∴AC=BC,DC=EC.
在△ADC和△BEC中,有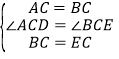 ,
,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠BEC=∠ADC.
∵点A,D,E在同一直线上,△CDE是等腰直角三角形,
∴∠CDE=∠CED=45°,∠ADC=180°﹣∠CDE=135°,
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°,
∴AD⊥BE.
③依照题意画出图形,如图(二)所示.

∵S△ABC+S△EBC=S△CAE+S△EAB ,
即![]() ACBC+
ACBC+![]() BECM=
BECM=![]() AE(CM+BE),
AE(CM+BE),
∴AC2﹣AEBE=CM(AE﹣BE).
∵△CDE为等腰直角三角形,
∴DE=2CM,
∴AE﹣BE=2CM,
∴CM=![]() .
.
(2)依照题意画出图形(三).

其中AB=![]() ,DP=1,BD=
,DP=1,BD=![]() AB=
AB=![]()
由勾股定理得:BP=![]() =3.
=3.
结合(1)③的结论可知:
AM=![]() =
=![]() =1.
=1.
故点A到BP的距离为1.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
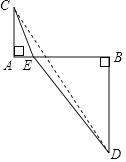
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分) 如图,小明把一张边长为![]() 厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,
厘米的正方形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子,

(1)如果要求长方体盒子的底面面积为![]() ,求剪去的小正方形边长为多少?
,求剪去的小正方形边长为多少?
(2)长方体盒子的侧面积是否可能为![]() ?为什么?
?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
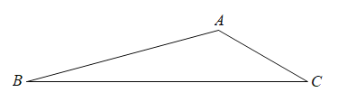
【题目】如图,在△ABC中,∠ABC![]() 15°,AB
15°,AB![]()
![]() ,BC
,BC![]() 2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
2,以AB为直角边向外作等腰直角△BAD,且∠BAD=90°;以BC为斜边向外作等腰直角△BEC,连接DE.
(1)按要求补全图形;
(2)求DE长;
(3)直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com