
【题目】已知![]() 的三边长
的三边长![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 都是整数,且
都是整数,且![]() ,
,![]() 的最大公约数为
的最大公约数为![]() .点
.点![]() 和点
和点![]() 分别为
分别为![]() 的重心和内心,且
的重心和内心,且![]() .则
.则![]() 的周长为________.
的周长为________.
【答案】![]()
【解析】
延长GI分别交BC于点P,AC于点Q,首先证明△CPQ为等腰三角形,根据内心和重心的知识分别表示出△PCQ的面积,进而求出a,b,c之间的等量关系式,最后对a,b,c进行讨论,进而求出a,b和c的值.
延长GI分别交BC于点P,AC于点Q,

∵∠GIC=90°,
∴GI⊥CI,I是内心,
∴△CPQ为等腰三角形,
∴PC=QC,
∴S△PCQ=2S△CQI=r×CQ(r为三角形ABC内切圆半径)
∴S△PCQ=S△PGC+S△CGQ=![]() PCha(ha为GE⊥BC的高)+
PCha(ha为GE⊥BC的高)+![]() CQhb(hb为GF⊥AC的高)=
CQhb(hb为GF⊥AC的高)=![]() CQ(ha+hb)=r×CQ,
CQ(ha+hb)=r×CQ,
∴2r=ha+hb①,
∵r=![]() ②,
②,
∵S△ABC=![]() ×aha'(ha'为AM⊥BC的高)=
×aha'(ha'为AM⊥BC的高)=![]() ×aha,
×aha,
∴ha=![]() ,hb=
,hb=![]() ,
,
∴ha+hb=![]() +
+![]() ③,
③,
把②③代入①得![]() ,
,
当a=2,b=2时,c=2,
∵△ABC为等边三角形,
∴GI重合,舍去,
∴a≠b,
设a>b,a=2m,b=2n,
∵a、b的最大公约数为2,
∴(m,n)=1,
∴m+n整除12,
即m=7,n=5,
∴a=14,b=10,c=11,
∴a+b+c=35.
故答案为:35


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个无人超市仓库的货物搬运工作全部由机器人![]() 和机器人
和机器人![]() 完成,工作记录显示机器人
完成,工作记录显示机器人![]() 比机器人
比机器人![]() 每小时多搬运50件货物.机器人
每小时多搬运50件货物.机器人![]() 搬运2000件货物与机器人
搬运2000件货物与机器人![]() 搬运1600件货物所用的时间相等,则机器人
搬运1600件货物所用的时间相等,则机器人![]() 每小时搬运货物( )
每小时搬运货物( )
A.250件B.200件C.150件D.100件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等边三角形,点D是AC边上动点,∠CBD=α,把△ABD沿BD对折,A对应点为A'.
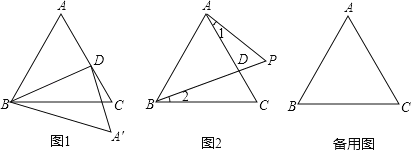
(1)①当α=15°时,∠CBA'= ;
②用α表示∠CBA'为 .
(2)如图2,点P在BD延长线上,且∠1=∠2=α.
①当0°<α<60°时,试探究AP,BP,CP之间是否存在一定数量关系,猜想并说明理由.
②BP=8,CP=n,则CA'= .(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM的长为x,CN的长为y,且x、y满足等式![]() (a>0)
(a>0)
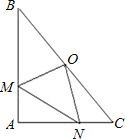
(1)求证:BM=AN;
(2)请你判断△OMN的形状,并证明你的结论;
(3)求证:当OM∥AC时,无论a取何正数,△OMN与△ABC面积的比总是定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.
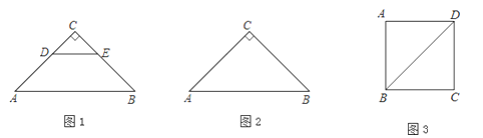
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为![]() , 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
, 若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 在坐标系中,
在坐标系中,![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,矩形
,矩形![]() 周长为18,面积为18.
周长为18,面积为18.

(1)求![]() 点坐标;
点坐标;
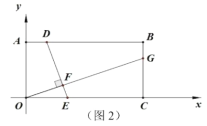
(2)如图2,![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,连
上,连![]() 、
、![]() ,若
,若![]() 于
于![]() ,
,![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
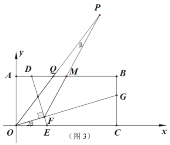
(3)如图3,在(2)的条件下,![]() 是
是![]() 中点,连
中点,连![]() 并延长
并延长![]() 至
至![]() ,连
,连![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com