
【题目】一个无人超市仓库的货物搬运工作全部由机器人![]() 和机器人
和机器人![]() 完成,工作记录显示机器人
完成,工作记录显示机器人![]() 比机器人
比机器人![]() 每小时多搬运50件货物.机器人
每小时多搬运50件货物.机器人![]() 搬运2000件货物与机器人
搬运2000件货物与机器人![]() 搬运1600件货物所用的时间相等,则机器人
搬运1600件货物所用的时间相等,则机器人![]() 每小时搬运货物( )
每小时搬运货物( )
A.250件B.200件C.150件D.100件
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=![]() (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中点,ED的延长线与CB的延长线相交于点F.
(1)求证:DF是BF和CF的比例中项;
(2)在AB上取一点G,如果AE·AC=AG·AD,求证:EG·CF=ED·DF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
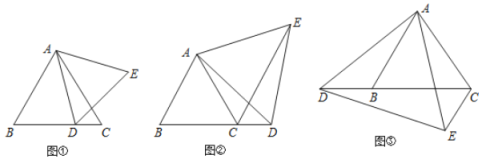
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
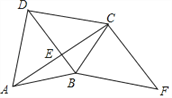
【题目】如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠CDB=45°,BD=2,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
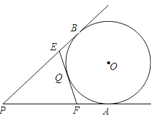
(1)求△PEF的周长.
(2)求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数与形是数学中的两个最古老,也是最基本的研究对象,它们在一定条件下可以互相转化.树形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.
(1) (思想应用)已知m, n均为正实数,且m+n=2求![]() 的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
的最小值通过分析,爱思考的小明想到了利用下面的构造解决此问题:如图, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,点E是线段AB上的动点,且不与端点重合,连接CE,DE,设AE=m, BE=n.
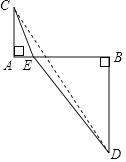
①用含m的代数式表示CE=_______, 用含n的代数式表示DE= ;
②据此求![]() 的最小值;
的最小值;
(2)(类比应用)根据上述的方法,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com